문제상황 및 데이터 살펴보기
- 경제 보고서 레퍼런스
- KB연구 보고서 : https://www.kbfg.com/kbresearch/index.do
- 다양한 Domain에 대한 보고서가 Data 기반으로 작성되어 있음 (1인가구보고서, 부자보고서 등등)
- 데이터로 증명된 보고서, 연구보고서뿐만 아니라 다양한 데이터가 있음
- 이를 관련해서 프로젝트를 진행해도 좋음 : 모두 무료로 개방이 되어있고, 조회수가 높진 않으며 양질의 데이터가 있음
- KB연구 보고서 외에도, 하나은행 금융경영연구소, 우리금융경영보고서, Gartner이라는 사이트가 있음
- 데이터적으로 ~한 시기에 와있구나를 인식하는 게 좋음
- 가격이 아니라 변동률! 률!!을 봐야한다. %가 중요함..! - 그래프를 볼 때, 담고 있는 정보 확인이 중요함!
- 그래프 파악하는 것에 공부를 하는 것이 좋음 : ~율 같은 것 조심해서 보기
- 판단은 거시적으로 하기
- 각각의 상관관계의 파악도 중요함! - 통계청 데이터보다 날것의 데이터를 보는 게 좋다! -> 가공도 쉽고, 보기가 좋음
- 전체 보고서에 대한 리뷰를 진행하면 좋음
Data Spec Check

- Boston 데이터 : 심플한 데이터!!!! 접근만 해서, 부동산 데이터의 플로우를 접근 방법을 공부하는 것
- public data이기에 데이터가 모두 살아있음 : feature을 모두 제공함
- boston 내에서 많은 지역들이 있는데, 각각의 동에 해당된다고 생각하면 됨
- 각각의 동에 대한 값이 raw
- 데이터 노이즈 없음!
- feature 네임에 대한 가공 X : 확인하기
- 동에 대한 중앙값 = y값 : 집하나에 대한 정보가 아닌, 동에 대한 정보이다.
문제해결 프로세스 정의
- 문제 상황 설명
1. 부동산은 사실 지역 정보 외 정보들이 영향을 미치는 경우가 많음
2. 주어진 데이터를 활용하여 최대한 지역을 대변할 수 있는 중요 변수로 데이터 셋을 구성함
3. 다양한 변수를 활용하여 Boston 집 값에 대한 중요한 변수를 찾아봄 - Check Point
- 세세한 것을 분석 할 때는 변수의 중요도도 중요하지만, 세밀하게 해석이 가능해야한다
: 복잡한 모델을 사용해서 Black Box를 열어보고 해석을 진행함
- Black Box를 까보는 것보다 그냥 Liner이나 DecisionTree같은 걸 진행해도 괜찮음!
- 재산, 값을 예상할 때는 완벽한 인터프리터 머신러닝 이용이좋을 수도 있다.
→ 거시적인 관점보다 미시적인 관점에서 Local한 Point를 찾아봄
→ 거시적인 관점에서 집 값의 전체적인 방향을 예측하려면 다른 변수들이 많이 필요함
→ 거시적인 관점에서는 금리, 분양가구, 미분양가구 등 다양한 변수 필요
→ 이러한 거시적 관점은 세밀한 데이터 분석보다 Domain과 오랜시간 쌓아온 경험이 필요함
: 경험이 없다면, fact 기반, data기반의 보고서를 많이 읽어야한다!!! 진짜 많이 읽어서 경험으로 만들어라.
→ 데이터의 Trend, Seasonality 등 긴 시간 동안의 Pattern 분석 필요
→ 따라서, 당장의 집 값을 예측하는 것 보다 긴시간을 두고 Trend를 예측하는 것이 필요함
→ 이번 데이터는 거시적인 분석 후 미시적인 분석으로 세밀하게 집값에 영향을 미치는 인자들을 도출해보는 시간을 갖음 - 기대효과
→ 세부적인 부동산 사항에서 중요 인자를 도출해봄
→ 부동산 가격 예측 및 원인분석에 대한 Insight와 노하우 축적 - 성과측정
→ 부동산 구매 후 가격 상승분 - 전체적인 Process
1. 전체적인 Trend를 알수 있는 데이터를 수집함(국토부, 부동산123 등)
→ 살것인가 말것인가
2. 거시적인 분석이 끝났으면 유망 지역을 선별하기 위해 미시적인 데이터 수집
→ 어떤지역을 살 것인가
가장 중요한 포인트!!!!!
* 거시적인 분석 -> 미시적인 분석
* 영향을 미치는 인자들의 도출을 확인해야함!
* 세밀한 데이터 분석보다는 fact, data 기반의 경험이 더 필요!
Data Info Check
데이터 정보에 대한 체크는 정말정말 중요하다!! 어떤 데이터를 담고 있는 걸 꼭 알아야한다!

- 보스턴 주택 가격 데이터셋의 일부
CRIM: 지역별 1인당 범죄율
- 높은 범죄율은 주거 환경의 안전성에 대한 우려로 이어져 집값에 부정적인 영향을 줄 가능성
- 범죄율이 높을수록 집값이 낮아지는 경향
ZN: 25,000 평방피트 이상의 주거 구역 비율
- 큰 집에 대한 비율 : 큰집이 얼마나 있는가
- 고급 주거지가 많음을 의미
- 집값에 긍정적인 영향
INDUS: 비소매 업종 구역 비율
- 상업 구역이 많을수록 주거 지역이 아닌 상업 지역으로 발전할 가능성이 크기 때문에, 집값에 부정적인 영향
- =상업지가 많은 지역의 경우, 주거 환경이 다소 열악
CHAS: 찰스강 인접 여부
- 강이랑 집이 닿아있으면 1, 아니면 0 : 1일수록 비쌀 확률이 높음
NOX: 일산화질소 농도 (백만분의 1 단위)
- 공기 오염도가 높을수록 주거 환경이 좋지 않기 때문에, 집값에 부정적인 영향
- NOX 농도가 높을수록 주택 가격이 낮아질 수 있음
RM: 주택당 평균 방 수
- 방의 개수가 많을수록 집이 넓고 크다는 의미이기 때문에, 집값에 긍정적인 영향
AGE: 1940년 이전에 건축된 소유 주택 비율
- 오래된 집이 많을수록 집값에 부정적인 영향
- 주택이 오래된 지역은 리모델링이나 유지보수가 필요한 경우가 많기 때문에, 집값이 낮아질 가능성
DIS: 5개의 보스턴 직업센터까지의 접근성 지수
- 도시 중심부로 부터 거리 : 접근지수가 높을수록 도심
- 고용 센터와 가까운 지역은 출퇴근이 편리해 인기가 높으
- 고용 센터와의 거리가 멀어질수록 집값에 부정적인 영향을 줄 가능성 있음
RAD: 방사형 도로까지의 접근성 지수
- 도시 중심부로 부터 거리 : 접근지수가 높을수록 도심
- 고속도로 접근성이 좋을수록 교통이 편리해 집값에 긍정적인 영향
- 지나치게 접근성이 좋으면 소음 등으로 인해 오히려 집값이 낮아질 수도 있음
TAX: 10,000달러당 재산세율
- 높을 수록 좋은 주택
- 재산세율이 높으면 집을 소유하는 비용이 높아지기 때문에 집값에 부정적인 영향을 미칠 가능성
PTRATIO: 지역별 학생-교사 비율
- 학생-교사 비율이 낮을수록 교육 환경이 좋다고 평가되며, 이는 집값에 긍정적인 영향
B: 1000(Bk-0.63)^2, 여기서 Bk는 자치시별 흑인의 비율을 말함.
- 당시 주택 시장의 인종적 편견이 포함된 변수
- 빼고 분석하는 게 좋을 듯함...
LSTAT: 모집단의 하위계층의 비율(%)
- 낮은 사회경제력 지위를 가진 인구 비율
- 하위 계층 비율이 높을수록 집값에 부정적인 영향을 미칠 가능성이 큼
- 낮은 사회경제적 지위를 가진 사람들이 많은 지역일수록 주거 환경에 대한 선호도가 낮음 - 높을수록 좋은 가능성이 높은 것
- ZN, CHAS, RM - 낮을수록 좋은 가능성이 높은 것
- CRIM, NOX, AGE, DIS, PTRATIO, LSTAT - 애매한 것
- INDUS, RAD, TAX, - *** MEDV: 주택 가격 중앙값 (천 달러 단위)
- 결과값!
Data Info Check Code
- 데이터 셋을 불러옴
from sklearn import datasets
X, y = datasets.fetch_openml('boston', return_X_y=True) # 보스턴 데이터셋을 불러온거- sklearn에서 제공해주는 dataset을 사용
- 코드는 X와 y라는 두 데이터프레임 또는 시리즈 객체를 열 방향(axis=1)으로 병합하는 코드
data = pd.concat([X, y], axis=1)
- pd.concat(): pandas 라이브러리의 concat 함수는 여러 개의 데이터프레임이나 시리즈를 지정된 축(axis) 방향으로 이어 붙임
- [X, y]: concat 함수에 병합할 데이터프레임 또는 시리즈들을 리스트로 전달
- axis=1은 열 방향으로 병합하라는 의미
- 데이터 파악하기
data # 데이터 보기
data.head() # 앞에 5개 보기
data.describe() # 데이터의 통계 요약 정보를 출력
- 데이터 정보 확인
data['INDUS'].unique().shape # ['~~']열에 존재하는 고유 값의 개수
data[data['LSTAT'] == 37.97] # '~~' 열의 값이 37.97인 행들을 필터링하여 반환
Counter(data['RAD']) # '~~' 열의 값들을 카운트하여 각 카테고리별 빈도수
data['MEDV'][data['RAD'] == '24'].mean() # 'RAD' 값이 24인 행들의 'MEDV' 열의 평균값을 계산합니다.
np.mean(data['MEDV'][data['CHAS'] == '0']) # 'CHAS' 값이 0인 행들의 'MEDV' 열의 평균값을 계산
np.mean(data['MEDV'][data['CHAS'] == '1']) # 'CHAS' 값이 1인 행들의 'MEDV' 열의 평균값을 계산
- 데이터 셋 크기를 plot으로 확인
plt.figure(figsize=(15,5))
sns.histplot(data['MEDV'], bins=50)
plt.show()
Data Readliness Check
- 데이터가 분석이나 모델링에 적합한 상태인지 평가하는 프로세스
- 데이터가 모델링 및 분석에 적합한지 검증하고, 이후의 분석 과정이 원활하게 진행될 수 있도록 기본적인 데이터 품질을 확보하는 중요
- 미싱 데이터 확인
-데이터프레임의 각 열에 대해 결측치 비율을 계산하여 리스트에 저장하는 과정
col = [] # 열 이름을 저장할 빈 리스트를 초기화
missing = []
for name in data.columns:
# Missing
missper = data[name].isnull().sum() / data.shape[0]
missing.append(round(missper, 4)) - missing = []: 결측치 비율을 저장할 빈 리스트를 초기화
- for name in data.columns: data 데이터프레임의 각 열(column)의 이름을 하나씩 가져옴
- missper = data[name].isnull().sum() / data.shape[0]: 결측치 개수를 전체 행 개수로 나누어 해당 열의 결측치 비율을 계산
- data[name].isnull().sum(): 해당 열의 결측치(null 값) 개수를 계산
- data.shape[0]: 데이터프레임의 전체 행(row) 개수
missing.append(round(missper, 4)): 결측치 비율을 소수점 네 자리로 반올림하여 missing 리스트
- 데이터프레임의 각 열에 대해 고유한 값의 개수를 계산하여 리스트에 저장하는 과정
col = []: 열 이름을 저장할 빈 리스트를 초기화
level = []
for name in data.columns:
# Leveling
lel = data[name].dropna()
level.append(len(list(set(lel))))
# Columns
col.append(name)- level = []: 각 열의 고유 값 개수를 저장할 빈 리스트를 초기화
- for name in data.columns: data 데이터프레임의 각 열(column)의 이름을 순회.
- lel = data[name].dropna(): 해당 열에서 결측치(null 값)를 제거하고 값이 있는 데이터만 남김.
- level.append(len(list(set(lel)))):
- set(lel): 결측치를 제거한 열의 값들로 고유 값들만 포함하는 집합을 만듬
- list(set(lel)): 집합을 리스트로 변환
- len(list(set(lel))): 리스트의 길이를 계산하여 해당 열에 있는 고유 값의 개수를 구한 후 level 리스트에 추가
- col.append(name): 열의 이름을 col 리스트에 추가
- 결측치 비율과 고유 값 개수에 대한 요약 정보를 담은 데이터프레임
- summary에는 각 열의 이름, 결측치 비율, 고유 값 개수가 정리된 하나의 데이터프레임이 생성
summary = pd.concat([pd.DataFrame(col, columns=['name']),
pd.DataFrame(missing, columns=['Missing Percentage']),
pd.DataFrame(level, columns=['Unique'])], axis=1)pd.DataFrame(col, columns=['name']): col 리스트를 데이터프레임으로 변환하며, 열 이름을 'name'으로 설정
-> col 리스트에는 각 열의 이름이 들어감
pd.DataFrame(missing, columns=['Missing Percentage']):
- missing 리스트를 데이터프레임으로 변환하며, 열 이름을 'Missing Percentage'로 설정.
- missing 리스트에는 각 열의 결측치 비율이 저장
pd.DataFrame(level, columns=['Unique']):
- level 리스트를 데이터프레임으로 변환하며, 열 이름을 'Unique'로 설정
- level 리스트에는 각 열의 고유 값 개수가 저장
pd.concat([...], axis=1):
- 세 개의 데이터프레임을 열 방향(axis=1)으로 이어붙여 하나의 데이터프레임을 생성
summary
-> summary는 name (이름) / Missing Percentage (결측치 비율) / Unique (고유 값 개수)를 갖는 표로 만들어짐!!!!
- 데이터를 정리(cutting)하여 분석에 불필요한 열을 제거
drop_col = summary['name'][(summary['Unique'] <= 1) | (summary['Missing Percentage'] >= 0.8)]
data.drop(columns=drop_col, inplace=True)
print(">>>> Data Shape : {}".format(data.shape))
summary['name'][(summary['Unique'] <= 1) | (summary['Missing Percentage'] >= 0.8)]:
- summary['Unique'] <= 1: Unique 열에서 고유 값이 1개 이하인 열을 찾음. (즉, 값이 하나만 존재하는 열을 의미)
- summary['Missing Percentage'] >= 0.8: Missing Percentage 열에서 결측치 비율이 80% 이상인 열을 찾습니다.
- | (or 연산자): 두 조건 중 하나라도 만족하는 열을 선택합니다.
-> drop_col 리스트에는 고유 값이 하나이거나 결측치 비율이 80% 이상인 열 이름들이 저장
data.drop(columns=drop_col, inplace=True):
- data.drop(columns=drop_col): drop_col에 포함된 열들을 data 데이터프레임에서 삭제
- inplace=True: 원본 data 데이터프레임에 바로 적용하여 변경사항을 저장
print(">>>> Data Shape : {}".format(data.shape)):
- 열을 제거한 후 데이터프레임의 크기가 어떻게 변했는지 확인
- 제거할 열의 개수를 반환
len(drop_col)- drop_col 리스트에 저장된 열 이름의 수를 나타내며, 조건에 맞는 (즉, 고유 값이 하나이거나 결측치 비율이 80% 이상인) 열이 몇 개인지 확인
Feature Engineering
- feature의 category에 대해서 공부가 필요!
- One Hotencoding
- 범주형 데이터를 머신러닝 모델에 적합한 수치형 데이터로 변환
- 범주형 변수의 각 고유 값을 별도의 열(column)로 변환하고, 해당 열에는 특정 행이 그 고유 값에 속하면 1, 그렇지 않으면 0을 할당
- One Hotencoding의 효과 파악 : category 변수를 알아듣게 encoding 해주는 것!
사용이유 : 머신러닝 모델은 수치 데이터를 입력으로 받기 때문에, 문자열이나 범주형 데이터를 그대로 사용할 수 없음
-> "색상"이라는 범주형 변수가 Red, Green, Blue의 값을 가질 경우, 이를 숫자형 데이터로 변환해 모델에 입력
- 이런 변환 과정에서 정보의 왜곡을 최소화하고 모델이 각 카테고리를 독립적으로 인식할 수 있도록 도움
장점 : 각 범주를 독립적으로 처리할 수 있어 범주형 데이터가 모델에 적합하게 변환, 정보의 왜곡 없이 모델이 범주 간의 관계를 독립적으로 이해 - 데이터의 타입을 확인
data.info()- 데이터는 float나 int 데이터이어야 분석에 사용 가능 : 이 외의 데이터를 바꾸는 작업이 필요함
- 바꾸기 이전에 바꿔야할 컬럼 확인
- 각 고유 값의 개수를 세어줌 :
Counter(data['CHAS'])
Counter(data['RAD'])- 값이 어떻게 분포되어 있는지 확인하여, 데이터 특성을 파악하고, 모델링 시 적절하게 처리할 수 있도록 돕기 위함
- CHAS : 이진 변수
- 선형 회귀 모델은 연속형 수치 데이터로 처리되는 경우 범주형 변수의 특성을 이해하지 못할수도 있음
- RAD : 다중 범주형 변수( 다수의 고유 값을 가질 수 있는 변수)
-> 둘다 적절한 인코딩이 필요함
- 특성(Feature)과 목표 변수(Target)로 분리하고, 일부 열을 모델이 잘 이해할 수 있도록 데이터 형 변환과 원-핫 인코딩을 적용
# X's & Y Split
Y = data['MEDV']
X = data.drop(columns=['MEDV'])
# CHAS는 0또는1 밖에 없기 때문에 int로 변환
# 그렇지 않으면 Liner regression에서 반응을 못함
X['CHAS'] = X['CHAS'].astype('int')
# RAD
X_dummy = pd.get_dummies(X, columns=['RAD'])
# RAD를 Int로 변형 시킨 후 정확도를 보기 위함
X['RAD'] = X['RAD'].astype('int')
Y : 주택 가격을 나타내는 목표 변수입니다. 여기서는 data 데이터프레임의 'MEDV' 열만 추출하여 Y에 저장
X: MEDV 열을 제외한 나머지 열들(즉, 모델의 특성(Features))로 구성된 데이터프레임
X['CHAS'] = X['CHAS'].astype('int') : 'CHAS' 열을 정수(int)형으로 변환
- CHAS 열은 값이 0과 1로만 구성된 범주형 변수로, 정수형(int)으로 변환하여 모델이 제대로 해석
- CHAS가 float 형태라면, 모델(특히, 선형 회귀 모델)이 범주형임을 인식하지 못할 수 있음
-> 정수형(int)으로 변환하여 명확히 범주형임을 표시해주는 역할
X_dummy = pd.get_dummies(X, columns=['RAD']) : 'RAD' 열에 원-핫 인코딩을 적용한 새로운 데이터프레임 X_dummy 생성
- RAD 열은 범주형 변수를 나타냄
- >pd.get_dummies()를 사용해 원-핫 인코딩을 적용하여 각 범주를 별도의 열로 변환.
- X_dummy는 원-핫 인코딩된 RAD 열을 포함한 데이터프레임으로, RAD의 고유 값들이 각각의 열로 분리
- 원-핫 인코딩(One-Hot Encoding)
- 범주형 데이터를 머신러닝 모델이 이해할 수 있는 수치 데이터로 변환하는 기법
- 범주형 변수의 각 고유 값을 0과 1로 이루어진 이진 벡터로 변환하여 모델에 입력
- 모델이 범주형 변수의 값을 독립적으로 처리하게 하여 수치형 변환의 오류를 방지
X['RAD'] = X['RAD'].astype('int') : 'RAD' 열을 정수(int)형으로 변환
- 정확도 확인을 위한 RAD 변환: RAD 열의 원래 값을 정수형(int)으로 변환
- 원-핫 인코딩을 적용하지 않은 X 데이터프레임에서도 RAD를 범주형 변수로 다루게 함
- 원-핫 인코딩을 적용한 경우(X_dummy)와 그렇지 않은 경우(X)의 모델 정확도를 비교하기 위해 준비한 것
- Y: 목표 변수(MEDV)를 저장.
- X: 특성(Features)을 저장하며, CHAS와 RAD 열을 정수형으로 변환.
- X_dummy: X에서 RAD 열에 원-핫 인코딩을 적용하여 범주형 변수를 인코딩한 데이터프레임.
- 잘 변환이 되었는지 확인
X_dummy.info()
X.info()- 각각에서 RAD와 CHAS가 int64로 바뀐 것을 확인가능
- 데이터셋을 훈련 데이터와 검증 데이터로 분할하여 학습 과정에서 모델 성능을 평가
- 전체 데이터를 훈련과 검증 세트로 나누고, 각각의 개수를 출력하여 데이터 분할 결과를 확인하는 과정
idx = list(range(X.shape[0]))
train_idx, valid_idx = train_test_split(idx, test_size=0.2, random_state=112)
print(">>>> # of Train data : {}".format(len(train_idx)))
print(">>>> # of valid data : {}".format(len(valid_idx)))- X.shape[0]: X 데이터프레임의 행 수. 이는 전체 데이터의 개수와 같음
- list(range(X.shape[0])): 데이터의 인덱스를 0부터 전체 데이터 개수까지의 리스트로 생성
train_test_split: scikit-learn 라이브러리의 함수로, 데이터를 랜덤하게 훈련 세트와 검증 세트로 분리
- idx: 전체 데이터의 인덱스 리스트를 입력으로 사용하여, 인덱스를 기준으로 데이터를 분할
- test_size=0.2: 전체 데이터의 20%를 검증 세트로 할당하고, 나머지 80%는 훈련 세트로 사용
- random_state=112: 분할 결과를 재현할 수 있도록 랜덤 시드를 설정하여, 항상 같은 방식으로 데이터를 분리
train_idx: 훈련 데이터의 인덱스 리스트.
-> print(">>>> # of Train data : {}".format(len(train_idx))) : Train data개수를 출력
valid_idx: 검증 데이터의 인덱스 리스트.
-> print(">>>> # of valid data : {}".format(len(valid_idx))) : valid data 개수를 출력
: 각 개수가 적당한지 확인하고 분석을 시작해야함
- 선형 회귀 모델(Linear Regression)을 훈련 데이터로 구축하고, 이를 학습하는 단계
- 훈련 데이터를 기반으로 선형 회귀 모델을 구축하고, 학습을 통해 최적의 회귀 계수를 계산
# Linear Regression 구축
model = sm.OLS(Y.iloc[train_idx], X.iloc[train_idx])
model_trained = model.fit()
sm.OLS(Y.iloc[train_idx], X.iloc[train_idx]):
- OLS 회귀는 잔차의 제곱합을 최소화하는 회귀 모델을 찾는 방법
- sm.OLS: statsmodels 라이브러리의 OLS(Ordinary Least Squares) 회귀 클래스를 사용하여 선형 회귀 모델을 생성
- Y.iloc[train_idx]: 목표 변수 Y의 훈련 데이터 인덱스(train_idx)에 해당하는 행만 선택하여 모델에 사용
- X.iloc[train_idx]: 특성 데이터 X의 훈련 데이터 인덱스(train_idx)에 해당하는 행만 선택하여 모델에 사용
model_trained = model.fit() : 모델 학습
- fit() 메서드는 모델을 학습시킵니다.
- 이 명령을 통해 model_trained는 훈련 데이터의 패턴을 학습한 훈련된 모델이 됨.
- model_trained에는 모델의 회귀 계수, 절편, 통계적 요약 정보 등이 포함되며, 예측과 결과 해석을 위해 사용.
- 훈련된 선형 회귀 모델에 대한 요약 통계 정보를 출력
print(model_trained.summary())
OLS(Ordinary Least Squares) 회귀 분석의 요약표
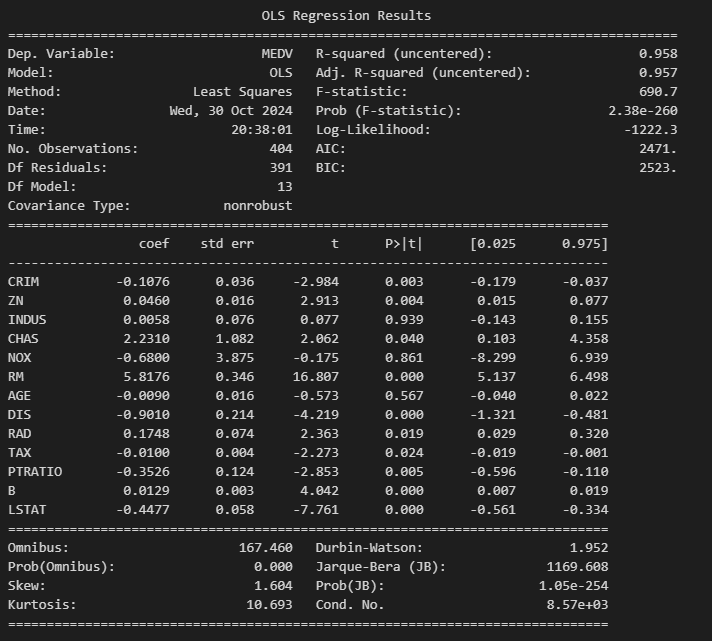
요약 부분
- Dep. Variable: 종속 변수(목표 변수)
- R-squared: 결정 계수 : 모델이 데이터를 얼마나 잘 설명하는지를 나타냄
- 높은 값일수록 모델이 데이터를 잘 설명
0.958 : 모델이 데이터를 95.8% 설명한다는 뜻
- Adj. R-squared: 수정된 결정 계수로, R-squared를 설명 변수의 개수에 맞춰 조정한 값
- 변수의 수가 많을 때, 높은 Adj. R-squared는 모델이 잘 맞는다는 것
- F-statistic 및 Prob (F-statistic): 모델 전체가 통계적으로 유의미한지를 검정하는 지표
- F-statistic: 690.7
- p-값(Prob): 2.38e-260 -> 0.05 이하일 경우 모델 전체가 통계적으로 유의미, 작을수록 좋은 값
- Log-Likelihood: 모델이 주어진 데이터를 얼마나 잘 설명하는지 나타내는 로그 가능도
- 값이 클수록 모델이 데이터를 잘 설명하는 경향
- 절대적인 임계값이 없고, 다른 모델들과 비교하여 Log-Likelihood 값이 클수록 더 나은 모델로 평가
- AIC (Akaike Information Criterion): 모델의 성능과 복잡성을 함께 고려한 지표
- 값이 작을수록 모델이 데이터를 더 잘 설명하고, 모델이 더 단순
- 절대적인 임계값 없음, AIC 값 차이가 2 이상이면 두 모델 간의 성능 차이가 있다고 봄
- BIC (Bayesian Information Criterion): AIC와 비슷하지만, 모델에 사용된 변수 수에 대해 더 엄격한 페널티를 부여
- 작을수록 좋은 값: 모델을 비교할 때 사용
- 절대적인 임계값 없음, BIC 값 차이가 2 이상이면 두 모델 간의 성능 차이가 있다고 봄
Coefficients Table (회귀 계수 테이블)
- coef : 각 특성의 회귀 계수
- 값이 클수록 MEDV에 미치는 영향이 큼.
- 양수이면 해당 특성이 MEDV에 양의 영향을 주고, 음수이면 음의 영향을 줌
- std err : 각 회귀 계수의 표준 오차
- 값이 작을수록 신뢰도가 높아집니다.
- t : 각 계수가 0이 아닌지를 검정하기 위한 t-값
- 큰 값일수록 유의미할 가능성 높음
- P>|t| (p-값) : p-value, 회귀 계수가 0일 가능성
- P>|t| 값이 0.05 미만인 특성들은 MEDV에 유의미한 영향을 미칩
- [0.025, 0.975] : 95% 신뢰 구간
- 이 구간에 0이 포함되지 않으면, 해당 계수가 통계적으로 유의미할 가능성이 높음
Diagnostic Information
Omnibus, Prob(Omnibus), Jarque-Bera (JB), Prob(JB): 잔차(오차)의 정규성을 검정하는 통계량
- p-값이 작으면(일반적으로 0.05보다 작을 때) 잔차가 정규분포를 따르지 않는다는 의미입니다.
Durbin-Watson: 잔차의 자기상관을 확인하는 지표
- 2에 가까울수록 자기상관이 적어 모델에 좋음. 이 값이 1.952로, 이상적에 가까움
Condition Number: 다중공선성(multicollinearity)의 정도
- 일반적으로 1000을 넘으면 다중공선성 문제가 있을 가능성이 있음
-> 이 경우 8.57e+03으로, 다중공선성 문제를 의심해볼 수 있다.
데이터 summary를 한 뒤에 봐야할 것!!!
요약
- 유의미한 특성: P>|t| 값이 0.05 미만인 특성들은 MEDV에 유의미한 영향을 미침
- 모델 적합도: R-squared와 Adjusted R-squared가 높아 모델의 설명력이 좋음.
- F-statistic 유의미성: p-값이 거의 0에 가까워 모델 전체가 통계적으로 유의미함.
- 다중공선성 문제: Condition Number가 높은 점을 고려해 일부 특성의 다중공선성을 점검할 필요가 있음.
- 원-핫 인코딩된 데이터를 사용하여 선형 회귀 모델을 구축하고 학습하는 과정
- 원-핫 인코딩을 적용한 경우와 적용하지 않은 경우 모델 성능을 비교하여, RAD 변수의 범주형 특성이 주택 가격 예측에 어떤 영향을 미치는지 평가
model_dummy = sm.OLS(Y.iloc[train_idx], X_dummy.iloc[train_idx])
model_dummy_trained = model_dummy.fit()model_dummy = sm.OLS(Y.iloc[train_idx], X_dummy.iloc[train_idx])
- sm.OLS: statsmodels 라이브러리의 Ordinary Least Squares(OLS) 회귀 클래스를 사용하여 선형 회귀 모델을 생성.
- Y.iloc[train_idx]: 목표 변수 Y에서 훈련 데이터 인덱스(train_idx)에 해당하는 데이터만 선택하여 사용.
- X_dummy.iloc[train_idx]: 원-핫 인코딩된 특성 데이터 X_dummy에서 훈련 데이터 인덱스에 해당하는 데이터만 선택하여 사용
model_dummy_trained = model_dummy.fit()
- model_dummy.fit(): 모델을 학습시키는 메서드로, 주어진 훈련 데이터를 사용하여 최적의 회귀 계수를 찾음.
- model_dummy_trained: 학습이 완료된 모델로, model_dummy_trained에는 회귀 계수, 절편, 통계 정보 등이 포함.
-> 이 모델을 통해 예측을 수행하거나 회귀 계수를 해석할 수 있음.
- 원-핫 인코딩된 데이터를 사용하여 학습한 선형 회귀 모델의 요약 통계 정보를 출력
print(model_dummy_trained.summary())
- 훈련 데이터와 테스트 데이터에 대한 예측값을 생성하는 부분
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
#y_train_pred = model_trained.predict(X.iloc[train_idx])
y_dummy_train_pred = model_dummy_trained.predict(X_dummy.iloc[train_idx])
#y_test_pred = model_trained.predict(X.iloc[valid_idx])
y_dummy_test_pred = model_dummy_trained.predict(X_dummy.iloc[valid_idx])
- model_dummy_trained.predict(X_dummy.iloc[train_idx]): 원-핫 인코딩된 훈련 데이터를 사용해 예측값을 생성
- y_dummy_train_pred는 훈련 데이터에 대한 예측값으로, 모델이 훈련 데이터에서 얼마나 잘 학습했는지 평가할 때 사용
- y_dummy_test_pred는 검증 데이터에 대한 예측값으로, 모델이 새로운 데이터에 대해 얼마나 잘 일반화되는지 평가할 때 사용
- 훈련 데이터에 대한 모델 성능 평가를 다양한 지표로 출력
print('Training MSE: {:.3f}'.format(mean_squared_error(Y.iloc[train_idx], y_train_pred)))
print('Training RMSE: {:.3f}'.format(np.sqrt(mean_squared_error(Y.iloc[train_idx], y_train_pred))))
print('Training MAE: {:.3f}'.format(mean_absolute_error(Y.iloc[train_idx], y_train_pred)))
print('Training R2: {:.3f}'.format(r2_score(Y.iloc[train_idx], y_train_pred))) - MSE (Mean Squared Error): 평균 제곱 오차로, 예측값과 실제 값의 차이를 제곱한 후 평균을 계산
- 값이 작을수록 예측값이 실제 값에 가깝다
- 큰 오차에 더 큰 페널티를 부여하므로, 오차를 최소화하는 데 유리
- 제곱을 통해 계산하기 때문에 이상치(outliers)에 매우 민감
- RMSE (Root Mean Squared Error): 평균 제곱 오차의 제곱근
- MSE와 비슷한 의미지만, RMSE는 오차의 단위가 실제 데이터의 단위와 동일하므로 해석이 더 직관적
- MSE와 같이 큰 오차에 대해 더 큰 페널티를 부여하면서도, 원래 데이터 단위로 해석
- MSE와 마찬가지로 이상치에 민감
- MAE (Mean Absolute Error): 평균 절대 오차로, 예측값과 실제 값 간의 차이의 절대값을 평균
- MSE보다 이상치의 영향을 덜 받으며, 값이 작을수록 예측이 실제 값에 가까움을 의미
- MSE와 RMSE에 비해 이상치에 덜 민감합니다. 이상치가 있더라도 MAE 값이 크게 변하지 않음
- 큰 오차와 작은 오차를 동일하게 취급하므로, 큰 오차에 대한 페널티가 작아질 수 있음
- R² Score: 결정 계수로, 모델이 데이터의 변동성을 얼마나 설명하는지를 나타내는 지표
- 값이 1에 가까울수록 모델이 데이터를 잘 설명
- 모델이 데이터를 얼마나 잘 설명하는지 직관적으로 알 수 있음. 여러 모델을 비교할 때 유용한 기준
- R² 값이 높다고 해서 반드시 좋은 모델인 것은 아님
- > 특히 과적합(overfitting) 모델의 경우 R² 값이 높을 수 있지만, 테스트 데이터에 대한 일반화 성능은 떨어질 수 있음
: 조정된 R² (Adjusted R²)을 사용하는 것이 좋다.
- 검증 데이터(테스트 데이터)에 대한 모델 성능 평가 지표를 출력
print('Testing MSE: {:.3f}'.format(mean_squared_error(Y.iloc[valid_idx], y_test_pred)))
print('Testing RMSE: {:.3f}'.format(np.sqrt(mean_squared_error(Y.iloc[valid_idx], y_test_pred))))
print('Testing MAE: {:.3f}'.format(mean_absolute_error(Y.iloc[valid_idx], y_test_pred)))
print('Testing R2: {:.3f}'.format(r2_score(Y.iloc[valid_idx], y_test_pred)))- 훈련 데이터에 대한 원-핫 인코딩된 모델의 성능을 평가하는 지표
print('Training MSE: {:.3f}'.format(mean_squared_error(Y.iloc[train_idx], y_dummy_train_pred)))
print('Training RMSE: {:.3f}'.format(np.sqrt(mean_squared_error(Y.iloc[train_idx], y_dummy_train_pred))))
print('Training MAE: {:.3f}'.format(mean_absolute_error(Y.iloc[train_idx], y_dummy_train_pred)))
print('Training R2: {:.3f}'.format(r2_score(Y.iloc[train_idx], y_dummy_train_pred)))- 검증 데이터에 대한 원-핫 인코딩된 모델의 성능을 평가하는 지표
print('Testing MSE: {:.3f}'.format(mean_squared_error(Y.iloc[valid_idx], y_dummy_test_pred)))
print('Testing RMSE: {:.3f}'.format(np.sqrt(mean_squared_error(Y.iloc[valid_idx], y_dummy_test_pred))))
print('Testing MAE: {:.3f}'.format(mean_absolute_error(Y.iloc[valid_idx], y_dummy_test_pred)))
print('Testing R2: {:.3f}'.format(r2_score(Y.iloc[valid_idx], y_dummy_test_pred)))
Modeling
- Boston Housing 데이터셋을 불러와 pandas DataFrame으로 변환하는 작업
from sklearn import datasets
X, y = datasets.fetch_openml('boston', return_X_y=True)
data = pd.concat([X, y], axis=1)- fetch_openml 함수로 데이터를 가져온 후, pd.concat을 사용하여 특성과 목표 변수
X, y = datasets.fetch_openml('boston', return_X_y=True)
- boston이라는 데이터셋을 OpenML에서 다운로드
- X : 특성(Features) 데이터를 의미하며, 보스턴 주택 데이터의 입력 변수들로 구성
- y : 목표 변수(Target) 데이터로, 주택 가격의 중앙값(MEDV)을 나타냄
- return_X_y=Tru : 데이터셋을 X와 y로 나누어 반환하겠다는 의미
data = pd.concat([X, y], axis=1)
- pd.concat : X와 y를 열 방향(axis=1)으로 연결하여 하나의 DataFrame으로 만듬
- data : 이제 X와 y가 하나의 데이터프레임으로 결합되었으며, data에는 보스턴 주택 데이터의 특성과 목표 변수가 포함
- 회귀 문제를 분류 문제로 변환하기 위해 MEDV (주택 가격의 중앙값) 변수를 상위 40%와 하위 40%로 나누는 작업
# Problem Convert
# Regression to Classifcation
# 상위 40% (Class 1)과 하위 40% (Class 0)
per_60 = np.percentile(data['MEDV'], 60)
per_40 = np.percentile(data['MEDV'], 40)
print(">>>> 60 Percentile : {}".format(per_60))
print(">>>> 40 Percentile : {}".format(per_40))- np.percentile(data['MEDV'], 60): MEDV 값에서 60번째 백분위수(퍼센타일)에 해당하는 값을 계산
- per_60는 MEDV의 상위 40%에 해당하는 경계값
- np.percentile(data['MEDV'], 40): MEDV 값에서 40번째 백분위수에 해당하는 값을 계산
- per_40는 MEDV의 하위 40%에 해당하는 경계값
- 데이터의 분포를 시각화
# Y Plotting
plt.figure(figsize=(15,5))
sns.histplot(data['MEDV'], bins=25)
plt.show()- plt.figure(figsize=(15,5)): 그래프의 크기를 설정
- 가로로 넓은 형태의 히스토그램이 생성되어 데이터의 분포를 더 잘 관찰
- sns.histplot(data['MEDV'], bins=25)
- sns.histplot: seaborn 라이브러리의 히스토그램 생성 함수
- data['MEDV']: MEDV 열을 입력으로 하여 MEDV 값의 분포를 시각화
- bins=25: 히스토그램의 막대(bin) 개수를 25개로 설정하여 데이터의 세부 분포
- plt.show(): 생성한 히스토그램을 화면에 출력
- 통계치 계산
data['MEDV'].mean() # MEDV 열의 평균값을 계산
np.percentile(data['MEDV'], 50) # MEDV의 중앙값을 계산- 회귀 문제를 분류 문제로 변환하고, 주택 가격이 높은 그룹과 낮은 그룹을 구분
# Data Selection
data = data[(data['MEDV'] >= per_60) | (data['MEDV'] <= per_40)]
data.reset_index(inplace=True, drop=True)
print('Data shape : {}'.format(data.shape))
- data['MEDV'] >= per_60: MEDV 값이 상위 40% 이상인 데이터만 선택
- data['MEDV'] <= per_40: MEDV 값이 하위 40% 이하인 데이터만 선택
- | 연산자: 상위 40% 또는 하위 40%에 속하는 데이터를 모두 선택하기 위해 OR 연산을 수행
- > MEDV가 상위 40% 또는 하위 40%에 속하는 데이터만 남기고, 나머지는 제거됩니다. 이로써 MEDV 값이 중간 수준에 해당하는 데이터는 제외
- data.reset_index(inplace=True, drop=True): 필터링 후 인덱스를 다시 설정하여 연속된 인덱스
- inplace=True: 기존 데이터프레임을 직접 수정
- drop=True: 기존의 인덱스 열을 삭제하고, 새 인덱스를 생성
- data.shape: 새로운 data 데이터프레임의 행(row)과 열(column)의 개수를 확인. 이를 통해 필터링 후 데이터의 크기를 파악
- 필터링된 MEDV 열의 값들을 히스토그램으로 시각화
# Y Plotting
plt.figure(figsize=(15,5))
sns.histplot(data['MEDV'], bins=50)
plt.show()- plt.figure(figsize=(15,5)): 그래프의 크기를 설정하여, 가로로 넓고 세로로 얇은 형태(15x5 인치)의 그래프를 생성
sns.histplot(data['MEDV'], bins=50)
- sns.histplot: seaborn의 히스토그램 함수로, MEDV 열의 분포를 시각화
- data['MEDV']: MEDV 열을 선택하여, 주택 가격이 필터링된 후 상위 40%와 하위 40%로 나뉜 상태에서의 분포
- bins=50: 히스토그램 막대(bin) 수를 50개로 설정하여 데이터의 분포를 세부적으로 나타냄
- 작은 변동까지 확인할 수 있어 데이터의 분포 특성을 더 잘 이해
- 회귀 문제를 이진 분류 문제로 변환하여, MEDV 값에 따라 상위 40%와 하위 40%를 분류하는 작업
data['Label'] = 3
data['Label'].iloc[np.where(data['MEDV'] >= per_60)[0]] = 1
data['Label'].iloc[np.where(data['MEDV'] <= per_40)[0]] = 0
print("Unique Label : {}".format(set(data['Label'])))- data['Label'] = 3
- 새로운 Label 열을 추가하고, 모든 값에 3을 할당하여 초기화합니다. 이렇게 하면 이후에 1과 0 레이블을 조건에 따라 쉽게 설정
- 상위 40%에 해당하는 행의 Label을 1로 설정
- 하위 40%에 해당하는 행의 Label을 0으로 설정
-> Label 열에 {0, 1}이 잘 할당되었는지 확인합니다. 출력 결과가 {0, 1}이라면 레이블 할당이 제대로 된 것
- 데이터 전처리 및 훈련/검증 데이터 분할을 수행
# Category 처리하기
data['CHAS'] = data['CHAS'].astype('int')
data = pd.get_dummies(data, columns=['RAD'])
# Data Split
Y = data['Label']
X = data.drop(columns=['MEDV', 'Label'])
idx = list(range(X.shape[0]))
train_idx, valid_idx = train_test_split(idx, test_size=0.2, random_state=119)
print(">>>> # of Train data : {}".format(len(train_idx)))
print(">>>> # of valid data : {}".format(len(valid_idx)))- 범주형 데이터 처리
1. CHAS 열을 정수형으로 변환: CHAS는 이진 변수(0 또는 1)를 나타내므로, 정수형으로 변환하여 모델이 잘 인식
2. RAD 열에 원-핫 인코딩 적용: pd.get_dummies를 사용하여 RAD 열의 각 고유 값을 별도의 열로 변환
데이터 분할
- 목표 변수 Y 설정: Label 열을 목표 변수로 설정
- 특성 변수 X 설정: MEDV와 Label 열을 제외한 나머지 열을 특성 변수로 설정
인덱스 생성 및 데이터 분할
- idx = list(range(X.shape[0])) : 전체 데이터 인덱스 생성: X의 행 수만큼 인덱스를 생성
- train_idx, valid_idx = train_test_split(idx, test_size=0.2, random_state=119)
- train_test_split을 사용하여 데이터 분할: 전체 인덱스를 훈련 세트와 검증 세트로 나눔
- test_size=0.2: 전체 데이터의 20%를 검증 세트로 사용
- random_state=119: 동일한 결과를 재현할 수 있도록 랜덤 시드를 설정
훈련 데이터와 검증 데이터의 크기 출력:
- print(">>>> # of Train data : {}".format(len(train_idx)))
- print(">>>> # of valid data : {}".format(len(valid_idx)))
-> 각각의 데이터 개수를 출력하여 데이터 분할이 제대로 되었는지 확인
- 결정 트리 모델의 최대 깊이(max_depth)를 2에서 10까지 변경하며 모델 성능을 평가하는 작업
# Parameter Searching ==> Depth 2 ~ 10
for i in range(2,11,1):
print(">>>> Depth {}".format(i))
model = DecisionTreeClassifier(max_depth=i, criterion='entropy')
model.fit(X.iloc[train_idx], Y.iloc[train_idx])
# Train Acc
y_pre_train = model.predict(X.iloc[train_idx])
cm_train = confusion_matrix(Y.iloc[train_idx], y_pre_train)
print("Train Confusion Matrix")
print(cm_train)
print("Train Acc : {}".format((cm_train[0,0] + cm_train[1,1])/cm_train.sum()))
# Test Acc
y_pre_test = model.predict(X.iloc[valid_idx])
cm_test = confusion_matrix(Y.iloc[valid_idx], y_pre_test)
print("Valid Confusion Matrix")
print(cm_test)
print("TesT Acc : {}".format((cm_test[0,0] + cm_test[1,1])/cm_test.sum()))
# Parameter Searching ==> Depth 2 ~ 10
- max_depth를 2부터 10까지 설정하여 결정 트리 모델을 학습하고 평가
- DecisionTreeClassifier: 결정 트리 분류 모델을 생성. 여기서 max_depth는 트리의 최대 깊이를 설정하며, criterion='entropy'는 정보 이득을 기준으로 분할을 수행.
- model.fit(...): 훈련 데이터를 사용하여 모델을 학습합니다.
# Train Acc
- 훈련 데이터에 대한 예측: X의 훈련 데이터로 예측을 수행
- 혼동 행렬 계산: confusion_matrix를 사용하여 훈련 데이터의 실제 레이블과 예측된 레이블을 비교.
- 혼동 행렬을 출력하고, 정확도를 계산하여 출력
# Test Acc
- 검증 데이터에 대한 예측: X의 검증 데이터로 예측을 수행
- 혼동 행렬을 계산하고 출력하며, 정확도를 계산하여 출력
Model evaluation and Summary
Regression -> classification : regression은 정답이 무한대이지만 classfication은 범주화!
- 결정 트리 모델을 최대 깊이 5로 설정하여 학습하는 과정
# Depth가 깊어질 수록 정확도는 높게 나오지만 해석력에 대한 가독성을 위해 Depth 4를 선택함
model = DecisionTreeClassifier(max_depth=5, criterion='entropy')
model.fit(X.iloc[train_idx], Y.iloc[train_idx])model = DecisionTreeClassifier(max_depth=5, criterion='entropy')
- DecisionTreeClassifier: 결정 트리 분류 모델을 생성
- max_depth=5: 트리의 최대 깊이를 5로 설정하여 모델의 복잡성을 제한.
- 깊이가 너무 깊어지면 모델이 과적합(overfitting)될 수 있으니 유의
- criterion='entropy': 분할 기준으로 엔트로피를 사용합니다. 이는 정보 이득을 기준으로 데이터를 분할하는 방법.
model.fit(X.iloc[train_idx], Y.iloc[train_idx])
- X.iloc[train_idx]와 Y.iloc[train_idx]를 사용하여 모델을 훈련 데이터로 학습
- X의 입력에 대해 Y의 클래스(상위 40% 또는 하위 40%)를 예측
- 결정 트리의 각 분기와 노드의 특성을 시각적으로 확인
from sklearn import tree
# Creating the tree plot
# Creating the tree plot (left = True, Right = False)
tree.plot_tree(model, filled=True, feature_names=X.columns, class_names = ['BAD', 'GOOD'])
plt.rcParams['figure.figsize'] = [40,10]tree.plot_tree(model, filled=True, feature_names=X.columns, class_names = ['BAD', 'GOOD'])
- tree.plot_tree: sklearn.tree 모듈의 함수를 사용하여 결정 트리 모델을 시각화
- model: 학습된 결정 트리 모델을 입력으로 사용
- filled=True: 각 노드의 색을 채워서 노드의 클래스 비율에 따라 색상이 다르게 표현
- feature_names=X.columns: 각 노드에서 사용되는 특성의 이름을 지정하여 그래프에 표시.
- class_names=['BAD', 'GOOD']: 클래스 레이블을 설정합니다. 여기서는 상위 40%를 'GOOD', 하위 40%를 'BAD'로 명명
plt.rcParams['figure.figsize'] = [40,10]
- plt.rcParams['figure.figsize']: 그래프의 크기를 설정
- 가로 크기를 40인치, 세로 크기를 10인치로 지정하여 넓은 트리 시각화
1차 스터디
공부방법
- 다른 기법도 공부해보기 ; 앙상블 기법 등등
- 다른 데이터에도 적용 시켜보기 : 캘리포니아 데이터
- ML 플로우 관련 공부하기
- 성능지표, 평가지표에 대해서 공부하기