* 강의를 듣고 필기한 내용일 이후에 따로 정리한 내용입니다.
Orientation
학습목표
- Statistics의 기초 개념과 원리, 방법을 토대로
- 기술통계 : 어떻게 수집한 데이터의 특성을 요약정리할 수 있는지,
- 추리통계 : 어떻게 분석한 데이터를 근거로 모집단의 특성을 추론할 수 있는지,
- 회기와 분류 : 어떻게 불확실한 미래의 사건을 예측할 수 있는지 를 학습하는 것
코스 소개
- 인공지능 분야에서 필수적인 확률과 통계에 대한 걔념과 원리를 학습
- Statistic는 데이터 분석, 패턴 익식, 의사 결정 등 다양한 인공지능 응용분야에서 중요한 역할을 함
- 확률과 통계의 기본걔념 이해, 이를 통해서 데이터를 효과적으로 요약및 분석하고 해석할 수 있는 능력 키우기
Rule of Sum & Rule of Product
합의 법칙과 곱의 법칙
- 합의 법칙 : 두 사건 A와 B가 상초배타적(동시 발생 불가)의 경우,
A가 일어나는 경우의 수가 m이고 B가 일어나는 경우의 수가 n이면, 사건 A또는 B가 일어나는 경우의 수는 m+n
- 정육면체 주사위를 한 번 던질 때, 짝수가 나오거나 홀수가 나오는 경우의 수 - 곱의 법칙 : 독립 사건 A와 B가 있을 때,
사건 A가 일어나는 경우의 수가 m이고, 사건 A의 각각의 결과에 대하여
독립적으로 사건 B가 일어나는 경우의 수가 n이면, 두 사건 A와 B가 동시에 일어나는 경우의 수는 m × n
- 서로 다른꽃병3개와장미6송이가있을때, 꽃병에장미를꽂기위해서꽃병한개와장미한송이를동시에택하는경우의수
Permutation & Combination
순열과 조합
- 순열 : 주어진 집합의 원소들을 특정한 순서로 배열하는 방법
순열에서는 원소의 순서가 매우 중요하며, 순서가 바뀌면 서로 다른 순열로 간주함
(집합{A,B}가 있을 때 가능한 순열은 AB와 BA, 두 순열은 다른 순열)
- 전체 순열 : 서로 다른 n개의 원소를 가진 집합에서 모든 원소를 사용하여 만들 수 있는 순열의 총 개수는 n팩토리얼로 계산함
- n팩토리얼: 1부터 n까지 자연수를 차례로 곱한 것을 n팩토리얼이라고 하며, 기호로는 n!과 같이 표기함
n! = n(n-1)(n-2) ....3X2X1
- 부분순열: 서로 다른 n개의원소 중에서 서로 다른r개를 선택하여 순서를 고려해 배열하는것
n개에서 r개를선택한 순열이라고하며,P(n,r)과 같이 표기함
-P(n,r) = n(n-1)(n-2)...(n-r+1) = n! / (n-r)! - 순열의 수에 대한 코드 표현
: import itertools : itertools는 Python의 표준 라이브러리 모듈 중 하나
- 효율적인 반복(iteration)을 위한 다양한 함수와 도구들을 제공함
: 해당 모듈은 반복자(iterators)를 생성하고 조합하여 복잡한 반복 작업을 단순하고 효율적으로 수행할 수 있게 도와줌
import itertools
lists = [1,2,3,4]
a = list(itertools.permutations(lists, 2))
print(a)
len(a)
-> a는 list에서 2개를 뽑아서 만들어낸 순열
[(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)]
12
- 조합 : 주어진 집합에서 순서에상관없이일부원소들을선택하는방법
조합에서는 원소의 순서가 중요하지 않으며, 순서가 바뀌어도 동일한 조합으로 간주함
- 집합{𝐴,𝐵}가 있을 때 가능한 조합은 원소 하나를 선택하는 경우 𝐴,𝐵
원소 두 개를 선택하는 경우 𝐴𝐵(즉, 조합에서는𝐴𝐵, 𝐵𝐴를동일한것으로취급)
- 서로 다른𝑛개의 원소 중에서 서로 다른 𝑟개를 선택하는 조합의 수를 𝑛개에서 𝑟개를 택한 조합
C(n,r) = n! / r!(n-r)! : - 조합의 수에 대한 코드 표현
import itertools
cards = [1, 2, 3, 4]
b = list(itertools.combinations(cards, 2)) # 리스트 생성
print(b)- itertools.combinations 함수를 사용하여 리스트 cards의 요소로 가능한 모든 2-요소 조합을 생성하는데, 이때 순서는 고려하지 않음(즉, (1, 2)는 (2, 1)과 같이 취급함)
- combinations 함수의 2번째 Argument는 선택할 요소의 수를 지정함
[(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)]
- 순열 : 순서를 고려하여 배열 하는 것
- 조합 : 순서에 상관없이 일부 원소를 선택하는 것
Probability Theory
확률의 기본 용어와 확률의 덧셈 법칙
확률 기본 용어
- 시행 : 동일한 조건에서 반복할 수 있으며, 그 결과가 우연에 의해 결정되는 관찰이나 실험
- 표본 공간: 시행에서 나타날 수 있는 모든 가능한 결과들의 전체 집합
- 근원 사건: 표본 공간을 구성하는 각각의 개별적인 결과, 즉 실험이나 시행에서 일어날 수 있는 단일한 사건
- 사건: 표본공간 내의 근원 사건들의 집합으로, 특정 실험이나 시행에서 발생 할 수 있는 결과들의 부분집합
- 합사건: 𝐴또는 𝐵가 발생하는 사건, 즉 둘 중 하나라도 발생하는 경우를 포함하는 사건
- 곱사건: 𝐴와 𝐵가 모두 동시에 발생하는 사건
- 배반사건: 𝐴와 𝐵가 동시에 발생 할 수 없고, 하나가 발생하면, 다른 하나는 반드시 발생하지 않는 사건
- 여사건: 사건𝐴 대해 𝐴가 일어나지 않는 경우에 해당하는 사건
수학적 확률
- 표본 공간 𝑆속의 모든 원소가 나올 가능성이 동일하고, 𝑛 (𝑆) = 𝑁, 사건𝐴에 대하여 𝑛 (𝐴) = 𝑛이면 𝐴의 확률은
- 모든 사건 𝐴에 대하여 확률𝑃(𝐴)는0 ≤ 𝑃(𝐴) ≤ 1
- 반드시 발생하는 사건 𝑆에 대하여 확률𝑃 (𝑆( = 1
- 절대로 발생하지 않는 사건∅에 대하여𝑃 (∅( = 0
통계적 확률 : 실제로는 더 많이 일어나는 사건
- 통계적 확률은 시행을 𝑁번하여 사건 𝐴가 일어난 횟수를 𝑟이라고 할 때,
𝑁을 충분히 크게 하면 상대도수로 나타나는 𝑟/𝑁이 일정한 확률값𝑃(𝐴)로 근사하게 된다는 것을 의미함
r / N = P(A) 이지만, lim r/N = P(A)
확률의 덧셈법칙 : 서로 다른 사건𝐴와 사건𝐵가 발생할 때, 𝐴또는𝐵가 일어날 확률
- P(AUB) = P(A) + P(B) -P(A교B)
- 배반사건의 경우 : P(AUB) = P(A) + P(B)
Learning objectives
조건부 확률
조건부 확률의 덧셈 법칙은 사건𝐴와 사건𝐵가 발생하는 과정에 순서 개념이 없음
- 사건𝐴가 발생한 상황 하에 사건𝐵가 발생할 확률을 구하고자 할 때, 조건부 확률을 구하게 되며, 𝑃(𝐵ㅣ𝐴)로 표기함
- 𝑃(𝐵ㅣ𝐴) = P(B교A) / P(A) , P(B교A) = 𝑃(𝐵ㅣ𝐴) X P(A)
- 독립사건일때 : 𝑃(𝐵ㅣ𝐴) = P(B|A여) = P(B) , P(B교A) = P(A)XP(B|A) = P(A) X P(B)
- 수학적 확률은 표본공간𝑆 속의 모든 원소가 나올 가능성이 동일하고
𝑛(𝑆) = 𝑁, 사건𝐴에 대하여 𝑛(𝐴) = 𝑛일때, 𝑃(𝐴) = 𝑛 / 𝑁 이 된다는 것을 의미 - 통계적 확률은 시행을 𝑁번하여 사건𝐴가 일어난 횟수를 𝑟이라고 할 때,
𝑁을 충분히 크게하면 상대도수로 나타나는 𝑟 / 𝑁 이 일정한 확률값𝑃(𝐴)로 근사하게 된다는 것을 의미 - 조건부 확률은 사건A가 발생한 상황하에 사건 B가 발생할 확률을 의미하며 𝑃(𝐵|𝐴)로 표기
Variables & Scales
변수, 데이터 척도
- 변수 : 변화하는 모든 수를 의미함
- 인과관계에 의하여 독립변수와 종속변수로 구분할 수 있음
- 독립변수와 종속변수
- 독립변수란 다른 변수에 영향을 주는 변수를 의미함
- 종속변수란 영향을 받는 변수, 즉 독립변수에 의하여 변화되는 변수를 의미
- 질적 변수 : 분류를 위하여 용어로 정의되는 변수
- 비서열 질적변수 : 서열이 정해질 수 없는 변수를 의미 (성별, 인종, 학력)
- 서열 질적변수 : 서열 질적변수란 서열적으로 구분할 수 있는 변수 (초졸, 중졸, 대졸)
- 양적 변수 : 양의 크기를 나타내기 위하여 수량으로 표시되는 변수
- 연속변수 : 주어진 범위 내에서 어떤 값도 가질 수 있는 변수 ( 체중, 나이, 키)
- 비연속변수 : 특정 수치만을 가질 수 있는 변수 (IQ점수, 만나이) - 척도 : 성격에 따라 크게 범주형 척도와 연속형 척도로 구분
- 범주형 척도 : 데이터들을 구분 지어 나눌 수 있는 척도
- 명목척도 : 수나 순서와 관계없이 이름만 붙여지는 척도 (남/여, 지역)
- 서열척도 : 숫자나 연산과는 관련이 없으나, 순서(서열)를 구분할 수 있는 척도 (1,2,3등, 메달, 학번)
- 연속형 척도 : 연속하는 속성의 데이터를 연구나 조사의 목적에 맞게 구분한 척도
- 등간척도 : 측정한 자료들을 대상으로 합과 차가 가능한 척도 ( 온도, 수학점수 등)
- 비율척도 : 등간척도의 성질과 함께 ‘없다’의 개념인 0값도 가지는 척도 (길이)
Population & Sampling
모집단과 표본추출
- 모집단 : 통계적연구대상이되는전체집합
- 모수 : 모집단을 분석하여 알아낸 결과 수치로 모집단의 특성값
( 모평균(𝜇), 모분산(𝜎 2 ), 모표준편차(𝜎) 등)
- 표본 : 모집단을 대표 할 수 있는 일부를 추출하여 연구나 조사를 실시하고자 할때 선택한 모집단의 일부
( 표본평균(𝑥), ҧ 표본분산(s 2 ), 표본표준편차(s) 등)
- 표본추출 방법
- 확률적 표본 추출 방법 : 동일한 확률 아래서 표본을 구성하는 방법
- 단순 무작위 표본 추출: 일정한 규칙을 적용하여 모집단으로부터 표본을 기계적으로 추출
- 체계적 표본 추출: 모집단을 대상으로 각각에 대해 번호를 제공하고 n개의간격으로 표본을 추출
- 비례층화 표본 추출: 모집단을 여러 개의 다른 집단으로 구분한 후, 각 집단의 구성을 고려하여 비례적으로 추출
- 다단계층화표본추출: 비례층화 표본 추출에서 상위-하위 표본단위를 설정한후 설정한값에 따라 다시 추출
- 군집 표본 추출: 모집단의 구성이 내부이 질적인 동시에 외부동질적으로 구성되어있을경우
모집단 전체를 조사하지 않고 몇 개의 군집을 표본으로 선택해서 조사
- 비확률적 표본 추출 방법 : 확률과 상관없이 연구자나 조사자가 자신의 생각대로 표본을 뽑거나 연구나 조사대상이 표본을구성하는 방법
- 편의 표본 추출 : 마음대로 추출
- 판단 표본추출: 연구자나 조사자가 적절하다고 판단된 구성원들을 표본으로 선정
- 할당 표본추출: 모집단의 속성을 대표 할 수 있는 연령, 학력, 직업등을 구분하여 결정한 후
각각에 대한 표본의 개수를 미리 정하여, 연구자나 조사자가 정한 표본의 개수에 따라 임의로 표본을 추출
- 자발적 표본 추출: 연구자나 조사자의 생각과는 달리 응답자가 원하여 직접 연구나 조사에 응하는 경우 표본으로 선정
Descriptive Statistics : 기술통계
데이터의 표현하는 방법 : 히스토그램, 원그래프, 상자수염그림
기술 통계 : 수집된 자료의 특성을 요약 정리하는것
- 통계? 여러가지 현상에 대해서수리적으로정리, 분석, 예측하는작업
- 기술통계 코드 표현 실습
import pandas as pd
df = pd.read_csv('gapminder.tsv', sep = '\t') # 데이터 셋 불러오기
df.loc[0] # 행선택, 이름으로 접근
df.iloc[0] # 행선택, 순서로 접근- 도수분포표 : 수집한 각각의 데이터에 빈도를 정리한 표를 의미함
- 직관적으로 인식되는 형태가 아니라 일일이 숫자를 비교해야한다는 단점이 있음
frequency_table = df.groupby('year')['pop'].sum().reset_index()
# 연도(year)를 기준으로 그룹화하고 인구(pop) 열의 도수분포표 생성- groupby : 데이터를 그룹 별로 구분하여 다루기 위해 사용하는 함수
- df.groupby(‘year’) [‘pop’]. sum(): df를 ‘year’열을 기준으로 그룹화한 후, 각 그룹 내에서‘pop’열의 값을 합산함
- reset_index(): 인덱스를 새로 설정하여, 데이터 프레임 형태로 변환
- 히스토그램 : 측정치들을 계급으로 구분하고 각 계급에 포함되는 측정치의 개수(도수)를 표현한 것
- 각 계급간의 상한과 하한이 서로 연결되기에 히스토그램의 막대 그래프는서로 붙어있는 형태로 표시함
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
df = pd.read_csv('gapminder.tsv', sep='\t') # 데이터셋 불러오기
plt.hist(df['lifeExp'], alpha = 0.3, bins=7, rwidth=2, color='red') #히스토그램 만들기- alpha= : 히스토그램바 색상의 투명도
- bins=: 히스토그램에 사용될 바의 수
- rwidth= : 각 바의 상대적인 너비
- color= : 히스토그램의 바 색상
- 원 그래프
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
df = pd.read_csv("gapminder.tsv", sep="\t") #데이터 불러오기
df2 = df.groupby('continent') #데이터의 일부
df2.describe() #정보(기술어) 불러오기
#원그래프 만들기
sizes = [624, 300, 396, 360, 24] # 원그래프에서 사용할 각 부분의크기
labels = [1, 2, 3, 4, 5] # 원그래프의 각 부분에 대한 레이블
colors = ['red', 'green', 'blue', 'yellow', 'purple']
plt.pie(sizes, labels = labels, colors = colors, autopct = '%.1f%%', shadow = False, startangle = 90 ) # 원그래프를생성
plt.axis('equal')
plt.show()- sizes = []: 원그래프에서 사용할 각 부분의 크기를 나타내는 리스트
- labels = []: 원그래프의 각 부분에 대한 레이블을 나타내는 리스트
- plt.pie(): 원그래프를 생성하는 함수
- autopct: 차트의 각 부분에 표시될 비율의 포맷을 지정
- shadow: 차트에 음영을 추가할지 여부를 지정
- startangle: 원그래프가 시작되는 각도를 지정
- plt.axis(‘equal’): 차트가 원형으로 표시되도록 축의 비율을 동등하게 설정
- Seaborn : matplotlib을 기반으로 구축된 데이터 시각화 라이브러리
- 상자수염그림 코드 표현
import pandas as pd
import matplotlib
import seaborn as sns
df = pd.read_csv('gapminder.tsv', sep='\t')
sns.boxplot(x='continent', y='lifeExp', data=df)- sns.boxplot(): 상자수염그림을생성하는함수
Descriptive statistic
기술통계량
- 기술통계량 : 통계량(statistic)은 표본을 분석하여 얻은 결과
- 기술(descriptive)하고자 하는 대상은 표본
- 표본이 모집단에 대한 대표성을 가지고 있음을 설명
- 통계량은 표본이 갖는 특성을 제공하며 이를 토대로 모수를 추정할 수 있는 기초자료가 됨 - 중심경향도 : 데이터들을 종합하여 그 중심을 이루는 값이 무엇인지를 구한 것
- 표본의 중심을 설명하는 것이기에 대표값
- 표본을 설명하고자 할 때 표본의 중심이 되는 값이 어느 정도 되는지 조사하고,
표본의 중심이 되는 값은 기준을 어떻게 정하느냐에 따라 달라질 수 있음
- 평균, 중앙값, 최빈값
- 평균 : 가장 많이 사용되는 중심 경향도, 모든 통계 분석에서 사용되며 표본의 특성을 살펴 볼 때 가장 먼저 확인하는 수치
- (산술평균) 평균으로부터 관찰값과의 편차의 합은 0임, 자료의 분포가 좌우대칭인 경우 평균과 중앙값은 동일함
- 중앙 값 : 관측된 자료의 편중과는 상관없이 최소값부터 최대값까지 나열했을 때 가운데 위치한 값
- 개수가 홀수일때 중앙값, 개수가 짝수일때 중앙 2개의 값의 평균
- 최빈값 : 표본에서 가장 많이 관찰되는 관측치
- 최빈값은 중심 경향의 측정치로 1개이상 존재할 수 있음, 자료중 평균이나 중앙값을 구하기 어려운 경우에 활용함 - 산포도 : 표본이퍼진정도를구성하는분포
- 분산, 표준편차, 범위, 등 - 정규 분포 : 통계학에서 가장 널리 사용되는 확률분포중 하나, 연속형확률변수가 특정한 패턴을 따르는 분포
- 연속형 확률변수: 특정구간 내의 모든 실수 값을 가질수 있는 변수
- 비대칭도 : 표본이 최대값이나 최소값에 몰려있는 정도, 왜도/첨도 - 모분산
- 표본의 분포 특성을 잘 드러내지 못하는 평균의 단점을 해소하기 위하여 평균과 각표 본들이 얼마나 떨어져있는 지를 측정한 차이(편차)를 확인
- 모평균과 모집단의 개별 측정치들 간의 차를 구하여 제곱하고 이를 모두 더한 후, 그 값을 다시 모집단을 구성하는 개수로 나누어 계산 - 표본분산 : 모집단을 기준으로 하지 않고, 표본을 선정하여 표본의 개수를(𝑛 − 1)로 계산한 분산
- (𝑛 −1)을 자유도 : 통계학에서 데이터를 분석할 때 독립적으로 변할 수 있는 값들의 수
- 표본의 개수 𝒏에서 1을 빼는 이유 : 표본평균을 계산할 때, 이미 하나의 제약 조건을 사용하기 때문 - 표본 표준편차 : 분산값에 루트(√분산값)를 씌워 제곱근을 만들면 표본표준편차가 됨
- 사분위수
- 측정값을 오름차순으로 작은 수부터 큰 수의 순서로 나열하고 누적 백분율을 4등분한 각 점의수치를 의미
- 제 1사분위 수는 누적 백분율25% 에 해당하는 값 = (𝑄1)=𝑛+1/4 번째 순위값
- 제 2사분위 수는 누적 백분율50% 에 해당하는 값 = (𝑄1)=𝑛+1/4X2 번째 순위값
- 제 3사분위 수는 누적 백분율75% 에 해당하는 값 = (𝑄1)=𝑛+1/4X3 번째 순위값
- 제 4사분위 수는 누적 백분율100%에 해당하는 값 = (𝑄1)=𝑛+1/4X4 번째 순위값
- 사분위 수의 범위 : 제3사분위 수–제1사분위 수
df['lifeExp'] # 열선택
df['lifeExp'].mean() # 열 평균
df['lifeExp'].max() # 열 최대값
df['lifeExp'].min() # 열 최솟값
df['lifeExp'].median() # 열 중간값
df['lifeExp'].var() # 열 분산
df['lifeExp'].std() # 열 표준편차
df['lifeExp'].describe() # 열을 계산한 정보 : count, mean, std, min, 25%, 50%, 75%, max, Name, dtype- df.mean() : 평균
- df.max() : 최대값
- df.min() : 최소값
- df.median() : 중앙값
- df.var() : 분산
- df.std() : 표준편차
- df.describe() : 기술통계요약
- 왜도
- 자료의 분포가 어느 정도로 비대칭적으로 분포되어 있는지를 나타내는 통계 지표임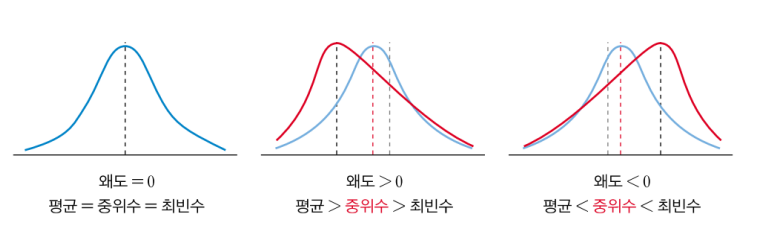
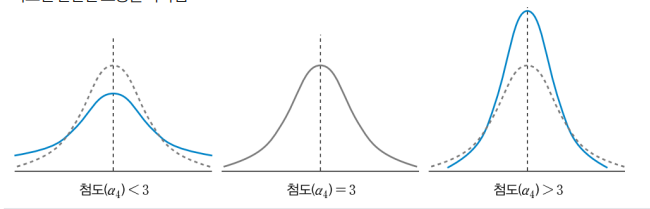
- 첨도
- 분포 곡선의 봉우리가 얼마 뾰족한지를 나타내는 수치임
'Upstage AI LAB 부트캠프 5기 > 실시간 공부내용 복습' 카테고리의 다른 글
| [2024.10.11] Statistics 기초 강의 (5) | 2024.10.11 |
|---|---|
| [2024.10.10] Statistics 기초 강의 (2) | 2024.10.10 |
| [2024.10.04] 파이썬 프로그래밍 이해하기 (8) | 2024.10.04 |
| [2024.10.01] 파이썬 프로그래밍 이해하기 (9) | 2024.10.02 |
| [2024.09.30] 파이썬 프로그래밍 이해하기 (10) | 2024.09.30 |