통계로 데이터 분석 이해하기_기초 통계량

[2024.10.08] 필수 온라인 강의 Part3 통계로 데이터분석 능숙해지기 CH01 기초통계량(1) 대푯값 , (2) 분산도

분포에 따른 평균, 중앙값, 최빈값의 관계

평균 (mean)

• 산술평균 : 흔히 평균이라고 부르는 값. 주어진 값들의 총합을 그 값들의 개수로 나누어 계산
• 기하평균 : 주어진 값들을 모두 곱한 후, 그 값들의 개수에 해당하는 n제곱근을 취해 계산, 비율이나 성장률을 다룰 때
• 조화평균 : 주어진 값들의 역수들의 산술평균을 구한 후, 그 값을 다시 역수로 변환한 값, 속도나 비율을 다룰 때
• 평균의 함정 : 평균이 모든 상황에서 유용한 통찰을 제공하지는 않으며, 잘못 해석될 가능성이 있음
                       - 다른 대표값들도 꼭 확인을 해줘야한다.
  
  

중앙값 (median)

• 데이터를 크기 순서대로 나열했을 때, 가장 가운데에 위치하는 값
• 데이터의 분포가 비대칭이거나 극단값이 있을 때 산술평균보다 데이터의 대표값을 더 잘 나타낼 수 있음
• 데이터가 짝수 개일 경우, 중간에 위치한 두 값의 평균을 중앙값으로 사용함

최빈값 (mode)

• 최빈값은 데이터 집합에서 가장 자주 등장하는 값을 의미
• 최빈값은 여러 개일 수도 있고, 모든 값이 한 번씩만 등장하는 경우에는 최빈값이 없을 수도 있음
  
  

파이썬으로 구해보는 기초 통계량

df.describe()              # 기초 통계를 불러오는 함수 : count, mean, std, min, max, 4분위수 출력

df.mean()                                  #산술평균
df.groupby('ym').컬럼.mean()               # 특정컬럼의 평균을 알아보는 법
df.groupby('ym').컬럼.sum()/df.groupby('ym').사고건수.count()     # 특정컬럼의 평균을 알아보는 법

df.median()                                    # 중앙값

df.mode()                                      # 최빈값

---

분산  & 표준편차

 

분산 : 데이터가 평균을 기준으로 얼마나 퍼져 있는지를 나타내는 지표

         - 데이터 값에서 평균을 뺀 차이를 제곱한 값들의 평균

         - 클수록 많이 퍼진 것, 작을 수록 안 퍼진 것

표준편차 : 데이터의 퍼짐 정도를 원래 데이터의 단위로 나타내는 지표
         - 분산의 제곱근

사분위 범위(IQR)과 이상치 탐지

사분위수(IQR) 값을 같은 개수 4개로 나눈 각각의 값 - 1사분위수 = Q1 : 25% - 2사분위수 = Q2 : 50%, median - 3사분위수 = Q3 : 75% - 사분위간 범위(Interquartile Range, IQR) : Q3 - Q1 - Maximum = Q3+1.5*IQR - Minimum = Q1 - 1.5*IQR - Outliers : 이상치, Min보다 작거나 Max보다 큰 값

 

변동계수

• 상대적으로 얼마나 변동이 많은지를 보기 위한 지표
• 단위가 다르거나, 표준편차가 비슷한 그룹끼리 비교하고 싶을 때 일정한 기준에 따른 비교가 가능
• 변동계수 (CV) = 표준편차 / 평균
  
  

왜도와 첨도

 

왜도 (Skeness)

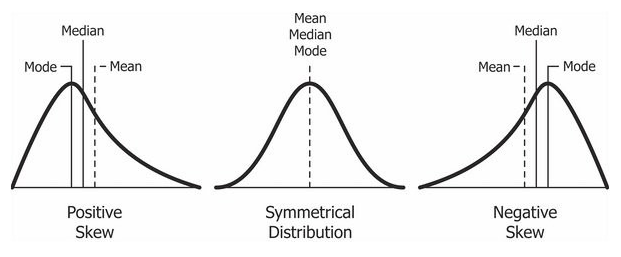
• 분석의 비대칭도를 나타내는 통계량
• 비대칭이 커질수록 왜도의 절대값은 증가
• 일반적으로 왜도가 -1~+1 범위는 치우침이 없는 데이터

첨도 (Kurtosis)

• 꼬리 부분의 길이와 중앙 부분의 뾰족함으로 데이터 분포를 알 수 있음
• Mesokurtic : 정규 분포 모양
  Leptokuric : 중앙 부분은 Mesokurtic보다 높고 뾰족하기 때문에 이상치(Outlier)가 많을수 있음
  Platykuric : Leptokuric와 반대, 이상치 (Outlier) 가 없음. 데이터 다시 확인 필요.

상자수염그림 파이썬으로 그려보기 

### 한글을 사용하므로 넣어줘야함 ###
!sudo apt-get install -y fonts-nanum
!sudo fc-cache -fv
!rm ~/.cache/matplotlib -rf

import pandas as pd 
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

from datetime import datetime 
from statsmodels.tsa.seasonal import seasonal_decompose

plt.rc('font', family='NanumBarunGothic')     # 한글 깨지면 폰트 지정해줌
plt.rcParams['figure.figsize'] = 15,8         # 그래프 사이즈 지정
plt.figure(figsize=(4,4))

df = pd.read_excel('/content/drive/MyDrive/data/도로교통공단_일자별 시군구별 교통사고 건수.xlsx')       # 데이터 불러옴
df.describe()           # 데이터 통계 불러오기

plt.boxplot(df['사고건수'])       # 박스 플롯 가져오기
plt.show()

fig, ax = plt.subplots()
ax.boxplot([df['사고건수'], df['중상자수']])         # 여러개의 박스 플롯 가져오기

plt.title('2020년 사고건수, 중상자수 Boxplot')           # 그래프 타이틀
plt.xticks([1, 2], ['사고건수', '중상자수'])             # 그래프 x축 라벨링
plt.show()

sns.boxplot(x='시도', y='사고건수', data=df)         #seaborn으로도 그래프를 볼 수 있다.
plt.show() 

sns.boxplot(x='시도', y='사고건수', hue='ym', data=df)       # hue는 그래프를 나눠줄수잇음
plt.show()

sns.boxplot(x='시도', y='사고건수', data=df, palette='Set3', linewidth=3, width=0.8)    # 그래프의 색상
plt.show()

sns.violinplot(x='시도', y='사고건수', data=df, palette='Set3')  # 그래프 모양을 바이올린 형으로
plt.show()