[2024.10.08] 필수 온라인 강의 Part3 통계로 데이터분석 능숙해지기 CH03 기술통계 , CH04 통계실험과 유의성 검정
모집단과 표본
모집단(Population)
- 통계를 통해 알고 싶어하는 모든 집단
- 모수(paramenter) : 모집단의 특성 (모평균, 모분산, 모표준편차 등)
표본(Sample)
- 모집단의 분포, 특성을 알기 위해 모집단에서 추출된 일부 집단
- 통계량(statistic) : 표본의 특성(표본평균, 표본 분산, 표본 표준편차 등)
추출(Sampling)
- 모집단에서 표본을 추출하는 방법
- 확률 표본 추출
- 단순 샘플링 (Simple Random Sampling) : 모든 요소가 동등한 확률로 선택될 수 있도록 무작위
- 층화 샘플링 (Stratified Sampling) : 모집단을 특정 기준에 따라 여러 '층'으로 나눈 후, 각 층에서 무작위 샘플링
- 계통 샘플링 (Systematic Sampling) : 모집단의 리스트에서 일정 간격을 두고 샘플을 선택하는 방법
- 군집 샘플링 (Cluster Sampling) : 모집단을 여러 '군집'으로 나눈 후, 그 중 일부 군집을 무작위로 선택하고, 선택된 군집 내의 모든 요소를 조사

추론(Inference)
- 표본 통계량으로 모집단의 특성을 추론
정규분포와 중심극한정리

- 정규 분포는 연속 확률 분포 중에서 가장 많이 사용
- 평균에 대해서 좌우 대칭, 평균에서 최대값, 종 모양
- 자연 현상이나 사회 여러 현상들이 정규 분포를 따른다.
- 정규 분포는 평균과 표준편차에 의해 결정된다.
중심 극한 정리
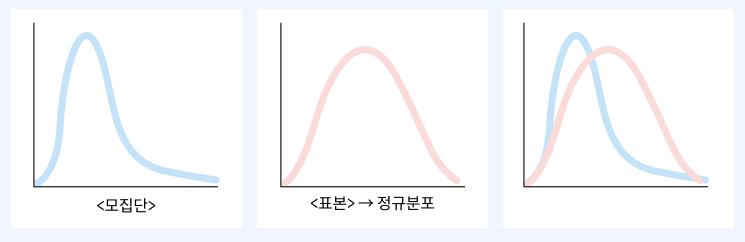
- 표본의 크기가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규분포에 가까워짐
- 표본 평균의 평균 = 모집단의 모평균
- 표본 평균의 표준편차 = 모집단의 모표준편차 / 표본크기의 제곱근
카이 제곱 분포
(chi-squared distribution, x² 분포)

- 검정 통계량이 카이제곱 분포를 따르는 통계 검정에 사용
- 분산의 특정을 확률 분포로 만든 것 : 마이너스가 없음
- 분포는 자유도에 의해 정의 : 자유도가 높을수록 정규분포에 근접 , 보통은 2~3정도다.
- 카이제곱 분포의 자유도가 높을수록 정규 분포에 근접
- y-skewed(y축에 편향된) 분포 : 그래프를 보기
- 제공된 값의 분산을 다루기 때문에, - 값은 존재하지 않고 + 값만 존재
스튜던트 t분포

- 모집단의 분산이 알려져 있지 않거나 소규모 표본일 경우 사용할 수 있음
- t-분포는 정규 분포와 비슷하지만, 표본의 크기가 작을 때 꼬리 부분이 더 두껍고 길다
- 표본의 크기가 30 이하일 때 t-분포를 사용
- t-분포가 널리 사용되는 이유 : 중심극한정리에 의해 보통 통계량은 정규 분포를 따르기 때문
- t-분포는 표본평균과 두 표본평균 사이의 차이, 회귀 파라미터 등의 분포를 위한 기준으로 사용
F분포
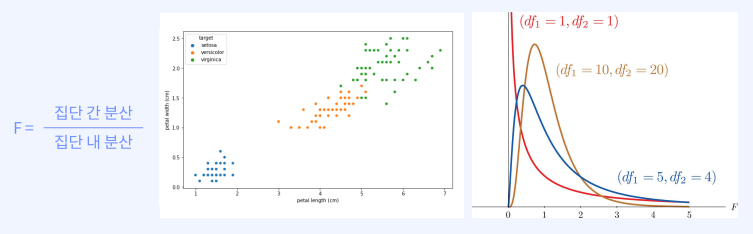
- 스튜던트 t 분포는 집단 3개 이상은 검정이 불가 → F 분포로 검정
- 집단간의 분산을 다룸
- 분산분석에 주로 사용
가설 검정
검정(Test) : 내가 세운 가설이 통계적으로 유의한지 살펴보는 것
- 검정 순서 : 귀무가설과 대립가설을 설정한다. -> p-value를 구한다. -> p-value를 기준으로 가설의 채택/기각 여부를 결정한다.
- 귀무가설 (Null hypothesis: H0)
- 검정 대상이 되는 가설
- 관습적이고 보수적인 가설
- 표본을 보고 "이러할 것이다."라고 세운 가설
- 연구자가 주장하고 싶은 대립가설과 반대되는 진술
- 귀무가설은 기각(Reject)이 목표 - 대립가설 (Alternative hypothesis: H1)
- 귀무가설에 대립되는 가설
- 지금까지 알려지지 않은 새로운 주장
- 연구자가 원하는 주장 혹은 가설
- 대립가설은 채택(accept)이 목표 - 귀무가설과 대립가설은 정반대이다
- P-value : 귀무가설이 참이라는 가정 하에서, 실제로 관찰된 데이터나 그보다 더 극단적인 결과가 나올 확률
- 작을수록 관찰된 결과가 우연에 의해 발생할 가능성이 적다는 것을 의미
- 값이 작다 : 귀무가설을 기각할 수 있는 증거가 강함 : 대립가설이 맞음
- 값이 크다 : 귀무가설을 기각할 수 없다 : 귀무가설이 맞다
- p-value ≤ 0.05: 통계적으로 유의미
- p-value > 0.05: 통계적으로 유의미하지 않음
ex) 어떤 실험에서 새로운 약물이 기존 약물보다 효과가 더 좋다는 가설을 세움, 실험 결과에서 p-value가 0.03
-> 이 가설이 맞을 확률이 97% , 새로운 약물이 효과가 더 좋을 확률이 97%이다. - 단측 검정 (one-tailed test) : 한 방향성으로 가능성이 크다고 생각될때
- 양측 검정 (two-tailed test) : 방향성은 모르겠지만, 차이가 있다고 생각이 될 때
- 검정에서 조심해야할 실수
- 제 1종 오류 : 귀무가설이 옳은데도 불구하고 이를 기각
우연에 의한 효과를 실제라고 생각하고 잘못된 결론, 설레발
- 제 2종 오류 : 귀무가설이 옳지 않은데도 이를 채택
실제 효과를 우연에 의한 효과라고 생각한 경우, 믿는 도끼에 발등

- t 검정 (t test)
- 모집단의 분산이나 표준편차를 알지 못할 때 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정
- “두 모집단의 평균간의 차이는 없다”라는 귀무가설과 “두 모집단의 평균 간에 차이가 있다”라는 대립가설 중 선택
- 평균으로 한다!라는 걸 알아야한다! 평균을 이용하는 검정이다!
- t 값 (t-value) : 검정에 이용되는 검정통계량, 두 집단의 차이의 평균(X)을 표준오차(SE)로 나눈 값
- 표준오차와 [표본평균차이의 차이]의 비율
- 기각역 (Critical Region) : 귀무가설이 기각되기 위한 검정통계량(t값)이 위치하는 범위
- 면적=α (유의수준)과 자유도(n-1)에 의해 결정
- 단측검정(one-tailed test)의 경우 기각역이 한 쪽에 존재, 양측검정(two-tailed test)의 경우 기각역이 양쪽에 존재
- 독립표본 t test : 서로 독립인 두 집단 비교

- 대응표본 t test : 동일 그룹에 어떤 처리 후 전후 비교
* 독립표본 t test 실습
if 표본의 크기가 10~30이면, 정규성 검정 -> 정규성이라면, 등분산 검정, 아니라면 순위합 검정
if 표본의 크기가 30 이상이면, 등분산 검정 -> 등분산이라면, 등분산 가정 독립표본 t test, 아니라면 이분산 가정 독립표본 t test
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
house_a = np.random.normal(6, 5, 40) #집값은 랜덤으로 생성
house_b = np.random.normal(3, 5, 40) #집값은 랜덤으로 생성
tmp1 = pd.concat([pd.DataFrame(['A']*40), pd.DataFrame(house_a.tolist())], axis=1) #데이터프레임 포멧으로 바꿔줌
tmp2 = pd.concat([pd.DataFrame(['B']*40), pd.DataFrame(house_b.tolist())], axis=1) #데이터프레임 포멧으로 바꿔줌
df.columns = ['grp', 'value'] # 컬럼 두개만 가져옴
sns.boxplot(x='grp', y='value', data=df) #seaborn으로 그래프를 그림
plt.show()
등분산 검정
귀무가설 : 수도권(grp A), 지방(grp B) 집값의 분산이 같다.
대립가설 : 수도권(grp A), 지방(grp B) 집값의 분산이 다르다
stats.levene(np.array(df[df['grp'] == 'A']['value']), np.array(df[df['grp'] == 'B']['value'])) #A와 B의 value만으로 같은지 확인
stats.ttest_ind(np.array(df[df['grp'] == 'A']['value'])
, np.array(df[df['grp'] == 'B']['value'])
, equal_var=True)LeveneResult(statistic=0.20332704798347626, pvalue=0.6532997090203332) : p-value>0.05
Ttest_indResult(statistic=3.566860440061266, pvalue=0.0006212594134944521) : p-value<0.05 귀무가설을 기각하고 채택가능
-> 수도권과 지방의 짒값이 차이가 존재한다.
Levene’s Test (등분산 검정) : 두 집단의 분산이 동일한지 검정하는 방법
분산분석 (ANOVA, Analysis of variance)
분산분석(Anova)
- 3개 이상의 다수 집단을 비교할 때 사용하는 검정 방법
 |
 |
등분산성 가정
- 집단 내 분산이 서로 비슷한가? 비슷해야 비교 가능 : 위 사례에서 B는 비교 불가
검정순서
- Omnibus F 검정 : 여러 집단 간의 평균 차이를 검정할 때 사용
- 두 개 이상의 집단 평균이 모두 동일한지, 아니면 적어도 하나의 집단이 다른 집단과 차이가 있는지를 판단
F값이 큰가? 차이가 있는가?
- one way Anova : 한 가지 요인(변수)에 대해 여러 집단의 평균을 비교
( 세그룹의 성적)
- two way Anova : 두 가지 요인(변수)에 대해 집단 간의 상호작용을 고려하여 평균을 비교하는 방식
(성별과 학벌에 따른 성적영향 비교 - post hoc 검정 : 구체적으로 얼마나 차이가 나는가?
- ANOVA에서 유의미한 결과가 나왔을 때, 구체적으로 차이가 있는지를 확인하기 위해 추가적으로 수행하는 검정 - 검정 실습
import pandas as pd
import seaborn as sns
import scipy.stats as stats
import matplotlib.pyplot as plt
from scipy.stats import shapiro
from scipy.stats import levene
from sklearn.datasets import load_iris
from statsmodels.stats.multicomp import pairwise_tukeyhsd
iris = load_iris() # iris 데이터 사용
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names) # 데이터랑 타겟을 붙여주는 작업
target_df = pd.DataFrame(data=iris.target, columns=['target']) # 데이터랑 타겟을 붙여주는 작업
df = pd.concat([iris_df, target_df], axis=1)
df.columns = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'] # 컬럼명 바꿔주기
sns.boxplot(x='target', y='sepal_width', data=df) # box플롯 그래프 만들기
plt.show()
일원 분산분석(One way ANOVA)
- 귀무가설 : 집단(target) 간의 sepal_width 차이가 없다.
- 대립가설 : 집단(target) 간의 sepal_width 차이가 있다.
1. 정규성 검정
- 귀무가설 : 정규분포를 따른다, 대립 가설 : 정규분포를 따르지 않는다.
print(shapiro(df.sepal_width[df.target==0])) #정규성검사를 할 때 shapiro를 쓴다.
print(shapiro(df.sepal_width[df.target==1])) #정규성검사를 할 때 shapiro를 쓴다.
print(shapiro(df.sepal_width[df.target==2])) #정규성검사를 할 때 shapiro를 쓴다.
(0.97171950340271, 0.2715264856815338) #귀무가설을 채택 -> 정규분포를 따름
(0.9741330742835999, 0.33798879384994507)
(0.9673910140991211, 0.1809043288230896)
2. 등분산성 검정
- 귀무가설 : 등분산성을 만족한다. , 대립 가설 : 등분산성을 만족하지 않는다
print(levene(df.sepal_width[df.target==0], df.sepal_width[df.target==1], df.sepal_width[df.target==2]))
LeveneResult(statistic=0.5902115655853319, pvalue=0.5555178984739075)
# p>0.05, 귀무가설 채택 : 등분산성 만족
3. 일원 분산 분석 (One way ANOVA)
stats.f_oneway(df.sepal_width[df.target==0], df.sepal_width[df.target==1], df.sepal_width[df.target==2])
F_onewayResult(statistic=49.160040089612075, pvalue=4.492017133309115e-17)
# p<0.05 -> 결론 : 귀무가설 기각, 대립가설 채택
집단(target) 간의 sepal_width 차이가 있다.
4. 사후분석 (Post-hoc) : 구체적으로 어떤 차이가 나는지 검증하는 방법
Family Wise Error Rate : 하나의 가설에서 1종 오류가 발생할 가능성, 가설 검정을 많이 할 수록 FWER은 증가
hsd = pairwise_tukeyhsd(df['sepal_width'], df['target'], alpha=0.05)
hsd.summary()| group1 | group2 | meandiff | p-adj | lower | upper | reject |
| 0 | 1 | -0.658 | 0.001 | -0.8189 | -0.4971 | True |
| 0 | 2 | -0.454 | 0.001 | -0.6149 | -0.2931 | True |
| 1 | 2 | 0.204 | 0.0088 | 0.0431 | 0.3649 | True |
카이제곱검정
- 카이제곱 통계량은 데이터 분포와 가정된 분포 사이의 차이를 나타내는 측정값
- 카이제곱 검정통계량이 카이제곱분포를 따른다면 카이제곱분포를 사용해서 검정 수행
- 카이제곱분포에서 일어나기 불가능한 일이면 귀무가설 기각, 대립가설 채택 : t검정이랑 동일
독립성 검정: 두 변수는 서로 연관성이 있는가?
적합성 검정: 실제 표본이 내가 가정한 분포와 같은가?
동일성 검정: 두 집단의 분포가 같은가?
카이제곱검정 순서:
1. 기대값을 구한다.
2. 카이제곱을 구한다: (관측값 - 기대값)을 제곱하여 기대값으로 나눈다.
3. 2번을 합하여 전체의 카이제곱 값을 구한다.
4. 카이제곱의 자유도를 구한다.
A/B test에 대부분 카이제곱검정을 사용함
- 카이제곱검정 실습
- 독립성 검정 : 모집단을 범주화하는 두 변수 A, B가 서로 독립적으로 측정값에 영향을 미치는지 여부를 검정
귀무가설 : 유저 A군과 B군이 C페이지에 진입하는 것은 관련이 없다.
대립가설 : 유저 A군과 B군이 C페이지에 진입하는 것은 관련이 있다.
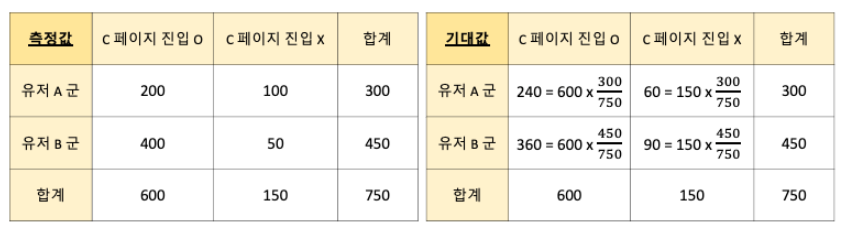
pow((200 - 240), 2)/240 + pow((100 - 60), 2)/60 + pow((400 - 360), 2)/360 + pow((50 - 90), 2)/90 # 테이블 설명
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
df = pd.DataFrame([[200, 100], [400, 50]], columns=['pv_t', 'pv_f']) # 데이터 프레임 불러오기
stats.chi2_contingency(observed=df) # 카이 제곱 검정을 진행
출력값 : (54.17534722222223, 1.833731033899248e-13, 1, array([[240., 60.], [360., 90.]]))
Chi-square : 54.17534722222223 # 카이제곱값
p-value : 1.833731033899248e-13 # p 값
df : 1 # 자유도
expected value : array : array([[240., 60.], [360., 90.]]))는 기댓값
-> p<0.05 : 귀무가설 기각, 대립가설 채택 : 유저 A군과 B군이 C페이지에 진입하는 것은 관련이 있다.
'Study > 통계' 카테고리의 다른 글
| 통계로 데이터 분석 이해하기_선형 회귀 분석 (7) | 2024.10.08 |
|---|---|
| 통계로 데이터 분석 이해하기_기초 통계량 (0) | 2024.10.08 |