[2024.10.08] 필수 온라인 강의 Part3 통계로 데이터분석 능숙해지기 CH05 선형 회귀 분석
단순 선형 회귀분석
- y = b0 +b1*x1
- 회귀 (Regression) : 독립변수(x)로 종속변수(y)를 예측하는 것
- 독립변수 (Independent variable) : 영향을 미칠 것으로 생각되는 변수
- 종속변수 (Dependent variable) : 영향을 받을 것으로 예상되는 변수
- 회귀계수 (Coefficient) 기울기와 절편
다중 선형 회귀분석
- 하나의 결과를 여러 원인으로 설명하기 위한 분석 방법
- y = b0 + b1*x1 + b2*x2 + b3*x3 + b4*x4 + ....+ bn*xn
- 결정 계수 (R-Squared)
R의 제곱 = 1 - SSE / SST , Adjusted R제곱 = 1 - (SSE/(n-p)) / (SST/(n-1))
- 독립변수가 종속변수를 얼마나 잘 설명해주는지 가리키는 지표.
- 0.5라 하면 독립변수가 종속변수의 50%정도를 설명한다고 함.
- 몇 퍼센트 이상이 실질적으로 유용하다고 말하기는 어렵고 어떤 분야에 따라 다름 (일반적으로 0.7 이상.)
- SSE (Explained Sum of Squares) : 추정값에서 관측값의 평균을 뺀 총 합
- SSR (Residual Sum of Squares) : 관측값에서 추정값을 뺀, 잔차의 총합
- SST (Total Sum of Squares) : 관측값에서 관측값의 평균을 뺀 결과의 총합
선형회귀의 기본적인 가정 5가지
- 오차 (Error) : 모집단에서 회귀식을 얻어서 회귀식을 통해 얻은 예측값과 관측값의 차이
- 잔차 (Residual) : 표본집단에서 회귀식을 얻어서 회귀식을 통해 얻은 예측값과 관측값의 차이
- 선형성 (Linearity) : 종속변수와 독립변수 간 선형적이어야 한다.
- 잔차 정규성 (Normality) : 잔차는 정규분포를 이루어야 한다.
- 독립성 (Independence) : 다중 선형회귀에만 해당하는 가정
- 독립변수는 서로 독립적이어야 한다.
- 다중 공선성과 밀접하게 연관되어 있다. - 다중 공선성 (Multicollinearity) : 다중 회귀분석을 수행할 경우 독립변수 간에 강한 상관관계가 없어야 한다.
- 등분산성 (Homoskedasticity) : 분산이 특정 패턴이 없이 일정해야 한다.
- RMSE( Root Mean Squared Error ): 회귀 분석에서 모델의 예측 성능을 평가할 때 사용하는 대표적인 지표
- RMSE는 예측 값과 실제 값 사이의 오차의 크기를 측정하며
이 오차들의 제곱 평균을 계산한 후, 그 값을 다시 제곱근으로 변환한 값을 의미
 |
|
다중 선형회귀분석 미니 프로젝트
import numpy as np #
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
from math import sqrt
from sklearn import preprocessing
from sklearn import datasets # 데이터를 받아와서 쓴다
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from statsmodels.stats.outliers_influence import variance_inflation_factor- 데이터 불러오기
dataset = datasets.load_boston() #데이터를 불러와서 씀
print(dataset.DESCR) #데이터를 정보를 확인함
df_x = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df_y = pd.DataFrame(dataset.target, columns=['MEDV'])
df = pd.concat([df_x, df_y], axis=1)- 데이터 기본 통계 확인
df.describe() # 데이터 기본통계를 확인함 : 한번은 보는 것을 추천- 데이터의 상관관계 확인
df.columns.values.tolist()
sns.pairplot(df[df.columns.values.tolist()]) # 각각 변수가 얼마나 상관관계가 있는지 확인
plt.show()
이런식으로 상관관계를 확인할 수 있다.
- 스케일링 진행
df.columns # 컬럼을 확인함
min_max_scaler = preprocessing.MinMaxScaler()
#스케일링 : 특정 minmax를 정해두고, 그 사이에서 움직인다고 정의하고 확인하는 방법
# 0~1 사이의 값으로 모든 값을 만듬
scale_columns = ['CRIM', 'ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
df_x[scale_columns] = min_max_scaler.fit_transform(df_x[scale_columns]) # 스케일링 데이터만듬- 데이터를 트레이닝 데이터와 테스트 데이터로 분할함
train_X, test_X, train_y, test_y = train_test_split(df_x, df_y, test_size = 0.3) # df_x와 df_y 데이터를 70%는 훈련 데이터로, 30%는 테스트 데이터로 분할- 선형 회귀 분석 수행하여, 모델의 요약 통계를 출력
m_reg = sm.OLS(train_y, train_X).fit()
print(m_reg.summary())
- 상단 요약 부분:
- Dep. Variable: MEDV (종속 변수), 여기서는 아마 주택 가격(Median value of owner-occupied homes)을 예측하는 모델
- Model: OLS, 최소자승법을 이용한 회귀 분석임을 나타냄
- Method: Least Squares(최소자승법).
- Date: 회귀 분석이 수행된 날짜와 시간.
- No. Observations: 354개의 관측값(데이터 포인트)이 사용
- Df Residuals: 잔차의 자유도, 즉 총 관측값에서 사용된 독립 변수의 개수를 뺀 값 (여기서는 354-13=341).
- Df Model: 모델에서 사용된 독립 변수의 개수, 13개
-Covariance Type: nonrobust, 이는 표준적인 공분산 추정 방법을 사용했음 - 모델 적합도 지표:
- R-squared: 0.957, 모델이 데이터의 95.7%의 변동을 설명할 수 있음. : 매우 높은 설명력을 보임
- Adj. R-squared: 0.956, 설명 변수가 많아질수록 R-squared를 과대평가하지 않도록 조정된 값.
- F-statistic: 586.4, 회귀 분석 모델의 전체 유의성을 평가하는 값. : 매우 높은 값을 보여 모델이 유의미함
- Prob (F-statistic): 2.79e-224, p-value : 0에 매우 가까운 값으로, 모델 전체가 통계적으로 유의미함.
- AIC/BIC: 모델의 적합도를 나타내는 정보 기준(Akaike Information Criterion 및 Bayesian Information Criterion)
두 값 모두 낮을수록 더 좋은 모델임 - 회귀 계수 (Coefficients): 독립 변수에 대한 회귀 계수와 그 통계적 유의성을 보여줌
- coef: 각 독립 변수의 회귀 계수입니다. 이 값들은 종속 변수(MEDV)에 미치는 독립 변수의 영향을 나타냄
(예, CRIM의 계수는 -12.3343, 이 변수의 값이 1 단위 증가할 때, 주택 가격은 약 12.33만큼 감소함.)
- std err: 회귀 계수의 표준 오차로, 이 값이 작을수록 해당 계수의 신뢰도가 높음
- t: t-통계량으로, 해당 회귀 계수가 0인지 아닌지를 검정하는 값
- P>|t|: 각 회귀 계수에 대한 p-value. 일반적으로 0.05보다 작은 p-value는 해당 변수가 통계적으로 유의미하다는 것을 의미
(예를 들어, CRIM의 p-value는 0.001로 유의미한 변수임을 보여줌)
- [0.025, 0.975]: 각 회귀 계수에 대한 95% 신뢰 구간. 이 범위에 회귀 계수의 실제 값이 존재할 가능성이 95%라는 것을 의미 - 잔차 분석:
Omnibus: 146.974, 잔차의 정규성을 검정하는 지표
Prob(Omnibus): 0.000, 정규성 가설을 기각할 수 있다는 것을 나타냄
Skewness: 1.534, 잔차의 왜도(비대칭성)를 나타냄. 0에 가까울수록 잔차가 정규분포에 가까움.
Kurtosis: 11.277, 잔차의 첨도(꼭대기의 뾰족함)를 나타냄. 3에 가까울수록 정규분포에 가까움
Durbin-Watson: 2.019, 잔차의 자기상관(autocorrelation)을 검정하는 지표. 값이 2에 가까울수록 자기상관이 없음을 의미
Jarque-Bera (JB): 잔차가 정규분포를 따르는지 여부를 검정하는 통계량.
- JB 값이 크면: 잔차가 정규분포를 따르지 않는다는 증거가 강하다는 의미
- JB 값이 작으면: 잔차가 정규분포에 가까운 형태라는 의미
- 여기서는 JB 값이 1149.454로 매우 큰 값을 보이고 있어, 잔차가 정규분포에서 크게 벗어나 있음을 의미.
Prob(JB): Jarque-Bera 검정 통계량에 대한 p-value
- p-value가 매우 작음: 일반적으로 0.05 미만이면 잔차가 정규분포를 따르지 않는다는 것을 강하게 시사.
- 여기서는 2.51e-250로, 매우 작은 값이므로, 잔차가 정규분포를 따르지 않는다는 강력한 증거입니다.
Cond. No (Condition Number): 다중공선성(multicollinearity)을 나타내는 지표
- 독립 변수들 간의 상관관계가 높을 때 경고 신호로 작용합니다. 값이 높을수록: 다중공선성이 의심될 수 있습니다.
- 일반적으로, 30을 넘는다면 다중공선성 문제가 있을 수 있다고 판단합니다.
- 여기서는 22.3으로, 다중공선성 문제가 발생할 가능성은 상대적으로 낮은 편입니다. - 예측된 값을 만들고자 함
pred_y = np.array(m_reg.predict(test_X)) # 예측 값을 배열로 변환
pred_y
pred_y = pred_y.reshape(pred_y.shape[0], 1) #데이터의 모양을 바꿔줌, 리스트로 바꿔줘야함 -> 1차원에서 2차원으로 변경
test_y = np.array(test_y) #실제 값를 NumPy 배열로 변환
print(sqrt(mean_squared_error(test_y, pred_y))) #MSE(Mean Squared Error)**를 계산, 예측 값과 실제 값 간의 오차를 제곱하여 평균을 낸 값- RMSE는 예측 값과 실제 값 간의 오차를 원래의 단위로 표현할 수 있도록 제곱근을 취한 값
- RMSE 값이 클수록 모델의 예측 성능이 좋지 않음을 의미하며, 값이 낮을수록 더 정확한 예측을 의미
- 상관관계 보기
train_X.corr() # 각각의 상관계수 확인
plt.figure(figsize=(12, 10))
sns.heatmap(train_X.corr(), annot = True, cmap = 'RdYlBu') # 각각의 상관계수를 보기 쉽게 히트맵으로
plt.show() |
 |
상관관계가 절대값이 1에 가까울수록 상관관계가 높음 : 상관관계가 높은 애들은 빼줘도 됌
- 분산 팽창계수 ( VIF (Variance Inflation Factor) ) 구하기
vif = pd.DataFrame() # 분산 팽창 계수
vif["VIF Factor"] = [variance_inflation_factor(train_X.values, i) for i in range(train_X.shape[1])] #VIF Factor라는 컬럼을 생성하여, 각 독립 변수에 대한 VIF 값을 저장
vif["features"] = train_X.columns
vif- VIF는 회귀 분석에서 다중공선성(multicollinearity) 여부를 확인하는 데 사용
- 각 독립 변수를 다른 독립 변수로 회귀 분석하여 계산
- 특정 독립 변수가 다른 변수들과 상관관계가 높을수록 VIF 값이 커짐
- 데이터 일부 빼기
tmp_train_X1 = train_X.drop('TAX', axis=1) #TAX가 빠진 데이터가 나옴
tmp_train_X1vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(tmp_train_X1.values, i) for i in range(tmp_train_X1.shape[1])] # 지운 데이터의 vif 재확인
vif["features"] = tmp_train_X1.columns
vif
train_x_tmp = train_X[vif['features'].tolist()] # 지운 데이터의 vif 선형 회귀 분석 재 수행
m_reg = sm.OLS(train_y, train_x_tmp).fit()
print(m_reg.summary())
test_X = test_X[train_x_tmp.columns.tolist()]
pred_y = np.array(m_reg.predict(test_X)).reshape(test_X.shape[0], 1)
test_y = np.array(test_y)
print(sqrt(mean_squared_error(test_y, pred_y)))- 재 확인하여, 얼마나 바뀌었는지 확인하면서 무엇을 지워야할지, 얼마나 지워야할지를 각각 알아냄
- 계속 확인하면서 얼마나 빼는 게 좋을지, 무엇을 빼는 게 좋을지 바꿔가면서 진행하는 게 맞음
plt.plot(pred_y, label = "pred")
plt.plot(test_y, label = "true")
plt.legend()
plt.show()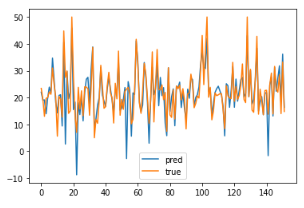
'Study > 통계' 카테고리의 다른 글
| 통계로 데이터 분석 이해하기_기술통계와 통계 실험 유의성 검정 (4) | 2024.10.08 |
|---|---|
| 통계로 데이터 분석 이해하기_기초 통계량 (0) | 2024.10.08 |